【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:

(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程: ![]() ,计算二次函数回归模型和线性回归模型的
,计算二次函数回归模型和线性回归模型的![]() 分别约为0.75和0.97,请用
分别约为0.75和0.97,请用![]() 说明选择个回归模型更合适,并用此模型预测
说明选择个回归模型更合适,并用此模型预测![]() 超市广告费支出为8万元时的销售额.
超市广告费支出为8万元时的销售额.
参考数据:  .
.
参考答案:
【答案】(1)![]() ;(2)对数回归模型更合适.当
;(2)对数回归模型更合适.当![]() 万元时,预测
万元时,预测![]() 超市销售额为
超市销售额为![]() 万元.
万元.
【解析】试题分析:(1)求出回归系数,可得![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)对数回归模型更合适.当![]() 万元时,预测
万元时,预测![]() 超市销售额为47.2万元
超市销售额为47.2万元
试题解析:
(1)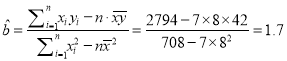
![]()
所以, ![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]()
(2)∵![]() ,∴对数回归模型更合适.
,∴对数回归模型更合适.
当![]() 万元时,预测
万元时,预测![]() 超市销售额为
超市销售额为![]() 万元.
万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
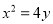 焦点为
焦点为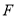 ,点A,B,C为该抛物线上不同的三点,且满足
,点A,B,C为该抛物线上不同的三点,且满足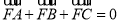 .
.(1)求
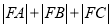 ;
;(2)若直线
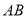 交
交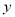 轴于点
轴于点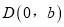 ,求实数
,求实数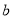 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是定义域为
是定义域为 的奇函数.
的奇函数.(1)求实数
 的值;
的值;(2)若
 ,不等式
,不等式 在
在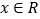 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;(3)若
 且
且
 上最小值为
上最小值为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,已知第一道审核、第二道审核、第三道审核通过的概率分别为
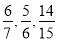 ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.(1)求审核过程中只进行两道程序就停止审核的概率;
(2)现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为
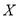 ,求X的分布列及数学期望.
,求X的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
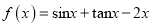 .
.(Ⅰ)证明:函数
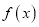 在
在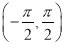 上单调递增;
上单调递增; (Ⅱ)若
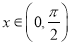 ,
, 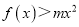 ,求
,求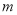 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
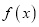 是定义在
是定义在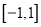 上的奇函数,且
上的奇函数,且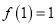 .若对任意的
.若对任意的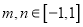 ,
, 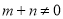 都有
都有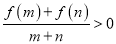 .
.(1)用函数单调性的定义证明:
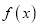 在定义域上为增函数;
在定义域上为增函数;(2)若
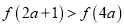 ,求
,求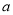 的取值范围;
的取值范围;(3)若不等式
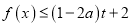 对所有的
对所有的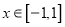 和
和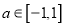 都恒成立,求实数
都恒成立,求实数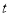 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是定义在R上的二次函数f(x)的部分图像,图2是函数
 的部分图像。
的部分图像。
(Ⅰ) 分别求出函数
 和
和 的解析式;
的解析式;(Ⅱ)如果函数
 在区间
在区间 上是单调递减函数,求
上是单调递减函数,求 的取值范围。
的取值范围。
相关试题

