【题目】育才高中为了推进新课程改革,满足不同层次学生的需求,决定在每周的周一、周三、周五的课外活动期间同时开设“茶艺”、“模拟驾驶”、“机器人制作”、“数学与生活”和“生物与环境”选修课,每位有兴趣的同学可以在任何一天参加任何一门科目.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各选修课各天的满座的概率如下表:
生物与环境 | 数学与生活 | 机器人制作 | 模拟驾驶 | 茶艺 | |
周一 |
|
|
|
|
|
周三 |
|
|
|
|
|
周五 |
|
|
|
|
|
(1)求茶艺选修课在周一、周三、周五都不满座的概率;
(2)设周三各选修课中满座的科目数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
试题分析:(1)根据相互独立事件的概率乘法公式易得茶艺选修课在周一、周三、周五都不满座的概率![]() ;(2)因为“生物与环境”、“数学与生活”、“机器人制作”、“模拟驾驶”满座的概率相等,所以可把这四科看成
;(2)因为“生物与环境”、“数学与生活”、“机器人制作”、“模拟驾驶”满座的概率相等,所以可把这四科看成![]() 次独立重复试验,与选修课“茶艺”按照相互独立事件求得随机变量
次独立重复试验,与选修课“茶艺”按照相互独立事件求得随机变量![]() 取每个值得概率,得到其分布列和数学期望.
取每个值得概率,得到其分布列和数学期望.
试题解析:(1)设茶艺在周一、周三、周五都不满座为事件A,
则![]() . ......2分
. ......2分
(2)![]() 的可能取值为0,1,2,3,4,5.
的可能取值为0,1,2,3,4,5.
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() . ......8分
. ......8分
所以,随机变量![]() 的分布列如下:
的分布列如下:
| 0 | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
|
......10分
故![]() ......12分
......12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
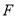 为抛物线
为抛物线 :
: 的焦点,点
的焦点,点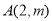 在抛物线
在抛物线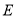 上,且到原点的距离为
上,且到原点的距离为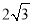 .
.(1)求抛物线
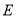 的方程;
的方程;(2)已知点
 ,延长
,延长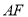 交抛物线
交抛物线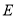 于点
于点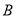 ,证明:以点
,证明:以点 为圆心且与直线
为圆心且与直线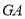 相切的圆,必与直线
相切的圆,必与直线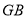 相切.
相切. -
科目: 来源: 题型:
查看答案和解析>>【题目】若有一个企业,70%的员工年收入1万元,25%的员工年收入3万元,5%的员工年收入11万元,则该企业员工的年收入的平均数是________万元,中位数是________万元,众数是________万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,且
,且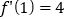 .
. (1)求函数
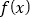 的极值;
的极值; (2)当
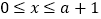 时,证明:
时,证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
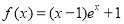 ,
,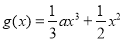 .
.(1)求
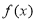 的单调区间及最小值;
的单调区间及最小值;(2)若在区间
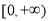 上不等式
上不等式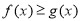 恒成立,求实数
恒成立,求实数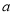 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
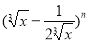 的展开式中,第6项为常数项.
的展开式中,第6项为常数项.(1)求
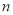 ;
;(2)求含
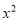 项的系数;
项的系数;(3)求展开式中所有的有理项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学在高考前各做了5次立定跳远测试,测得甲的成绩如下(单位:米):2.20,2.30,2.30,2.40,2.30,若甲、乙两人的平均成绩相同,乙的成绩的方差是0.005,那么甲、乙两人成绩较稳定的是________.
相关试题

