【题目】判断下列函数的奇偶性:
(1)f(x)=x+1;
(2)f(x)=x3+3x,x∈[-4,4);
(3)f(x)=|x-2|-|x+2|;
(4)f(x)=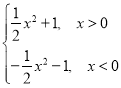
参考答案:
【答案】(1)既不是奇函数又不是偶函数;(2)既不是奇函数又不是偶函数;(3)奇函数;(4)奇函数.
【解析】
根据函数的奇偶性的定义,结合函数的解析式,逐个判定,即可求解.
(1)函数f(x)=x+1的定义域为实数集R,关于原点对称.
因为f(-x)=-x+1=-(x-1),-f(x)=-(x+1),即f(-x)≠-f(x),f(-x)≠f(x),
所以函数f(x)=x+1既不是奇函数又不是偶函数.
(2)因为函数的定义域不关于原点对称,即存在-4∈[-4,4),而4[-4,4),
所以函数f(x)=x3+3x,x∈[-4,4)既不是奇函数又不是偶函数.
(3)函数f(x)=|x-2|-|x+2|的定义域为实数集R,关于原点对称.
因为f(-x)=|-x-2|-|-x+2|=|x+2|-|x-2|=-(|x-2|-|x+2|)=-f(x),
所以函数f(x)=|x-2|-|x+2|是奇函数.
(4)函数的定义域为(-∞,0)∪(0,+∞),关于原点对称.
当x>0时,-x<0,f(-x)=-![]() (-x)2-1=-(
(-x)2-1=-(![]() x2+1)=-f(x);
x2+1)=-f(x);
当x<0时,-x>0,f(-x)=![]() (-x)2+1=
(-x)2+1=![]() x2+1=-(-
x2+1=-(-![]() x2-1)=-f(x).
x2-1)=-f(x).
综上可知,函数f(x)=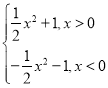 是奇函数.
是奇函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按照《国务院关于印发“十三五”节能减排综合工作方案的通知》(国发〔2016〕74号)的要求,到2020年,全国二氧化硫排放总量要控制在1580万吨以内,要比2015年下降15%.假设“十三五”期间每一年二氧化硫排放总量下降的百分比都相等,2015年后第
 年的二氧化硫律放总量最大值为
年的二氧化硫律放总量最大值为 万吨.
万吨.(1)求
 的解析式;
的解析式;(2)求2019年全国二氧化赖持放总量要控制在多少万晚以内(精确到1万吨).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
(2)已知函数f(x)=ax2+2x是奇函数,则实数a=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E、F分别是PC、AD中点,
(1)求证:DE//平面PFB;
(2)求PB与面PCD所成角的正切值。

-
科目: 来源: 题型:
查看答案和解析>>【题目】某地发生地质灾害,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为m的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足
 ,其中
,其中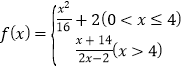 ,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化.(1)如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在7天(从投放药剂算起包括7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量m的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设动圆P(圆心为P)经过定点(0,2)、(t+2,0)、(t-2,0)三点,当t变化时,P的轨迹为曲线C
(1) 求C的方程
(2) 过点(0,2)且不垂直于坐标轴的直线l与C交于A、B两点,B点关于y轴的对称点为D,求证:直线AD经过定点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点,
 ,PA=AC=1.
,PA=AC=1.(1)求证:AE⊥PB;
(2)求三棱锥C-ABE的体积.
(3)求二面角A-PB-C的正弦值.

相关试题

