【题目】为了调查患胃病是否与生活规律有关,在某地对![]() 名
名![]() 岁以上的人进行了调查,结果是:患胃病者生活不规律的共
岁以上的人进行了调查,结果是:患胃病者生活不规律的共![]() 人,患胃病者生活规律的共
人,患胃病者生活规律的共![]() 人,未患胃病者生活不规律的共
人,未患胃病者生活不规律的共![]() 人,未患胃病者生活规律的共
人,未患胃病者生活规律的共![]() 人.
人.
(1)根据以上数据列出![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过![]() 的前提下认为“
的前提下认为“![]() 岁以上的人患胃病与否和生活规律有关系?”
岁以上的人患胃病与否和生活规律有关系?”
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
参考答案:
【答案】(1)见解析;(2)见解析
【解析】分析:(1)由已知作出![]() 列联表即可;
列联表即可;
(2)由列联表,结合计算公式,求得![]() =
=![]() ,,由此判断出两个量之间的关系.
,,由此判断出两个量之间的关系.
详解:
(1)由已知可列2×2列联表:
患胃病 | 未患胃病 | 总计 | |
生活规律 | 20 | 200 | 220 |
生活不规律 | 60 | 260 | 320 |
总计 | 80 | 460 | 540 |
(2)根据列联表中的数据,得K2的观测值![]()
![]() ,
,
因为9.638>6.635,因此在犯错误的概率不超过0.01的前提下认为“40岁以上的人患胃病与否和生活规律有关”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义运算:
 ,例如:34=3,(﹣2)4=4,则函数f(x)=x2(2x﹣x2)的最大值为 .
,例如:34=3,(﹣2)4=4,则函数f(x)=x2(2x﹣x2)的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,求
时,求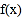 在区间
在区间 上的最值;
上的最值;(2)讨论函数
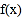 的单调性;
的单调性;(3)当
 时,有
时,有 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=ex﹣2x﹣a在R上有两个零点,则实数a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了
 月
月 日至
日至 月
月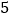 日的每天昼夜温差与实验室每天每
日的每天昼夜温差与实验室每天每 颗种子中的发芽数,得到如下资料:
颗种子中的发芽数,得到如下资料:日期
 月
月 日
日 月
月 日
日 月
月 日
日 月
月 日
日 月
月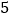 日
日温差






发芽数
 (颗)
(颗)




该农科所确定的研究方案是:先从这
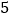 组数据中选取
组数据中选取 组,用剩下的
组,用剩下的 组数据求线性回归方程,再对被选取的
组数据求线性回归方程,再对被选取的 组数据进行检验.
组数据进行检验.(1)求选取的
 组数据恰好是不相邻两天数据的概率;
组数据恰好是不相邻两天数据的概率;(2)若选取的是
 月
月 日与
日与 月
月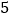 日的数据,请根据
日的数据,请根据 月
月 日至
日至 月
月 日的数据求出
日的数据求出 关于
关于 的线性回归方程
的线性回归方程 ;
;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过
 颗.则认为得到的线性回归方程是可靠的.试问(2)中所得到的线性回归方程是可靠的吗?
颗.则认为得到的线性回归方程是可靠的.试问(2)中所得到的线性回归方程是可靠的吗?附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的某种产品中抽取
 件,测量这些产品的一项质量指标值,由测量结果得如频率分布直方图:
件,测量这些产品的一项质量指标值,由测量结果得如频率分布直方图: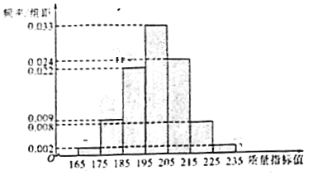
(1)求这
 件产品质量指标值的样本平均数
件产品质量指标值的样本平均数 和样本方差
和样本方差 (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);(2)由直方图可以认为,这种产品的质量指标值
 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .
.①利用该正态分布,求
 ;
;②某用户从该企业购买了
 件这种产品,记
件这种产品,记 表示这
表示这 件产品中质量指标值位于区间
件产品中质量指标值位于区间 的产品件数.利用①的结果,求
的产品件数.利用①的结果,求 .
.附:
 .若
.若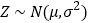 ,则
,则 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮
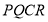 ,其中P是弧TN上一点.设
,其中P是弧TN上一点.设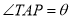 ,长方形
,长方形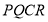 的面积为S平方米.
的面积为S平方米.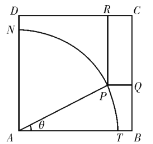
(1)求
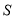 关于
关于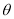 的函数解析式;
的函数解析式;(2)求
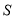 的最大值.
的最大值.
相关试题

