【题目】已知函数![]() ,设
,设![]() 为曲线
为曲线![]() 在点
在点![]() 处的切线,其中
处的切线,其中![]() .
.
(Ⅰ)求直线![]() 的方程(用
的方程(用![]() 表示);
表示);
(Ⅱ)求直线![]() 在
在![]() 轴上的截距的取值范围;
轴上的截距的取值范围;
(Ⅲ)设直线![]() 分别与曲线
分别与曲线![]() 和射线
和射线![]() (
(![]() )交于
)交于![]() ,
, ![]() 两点,求
两点,求![]() 的最小值及此时
的最小值及此时![]() 的值.
的值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ)![]() ,
, ![]() .
.
【解析】试题分析:(Ⅰ) 对![]() 求导数
求导数![]() ,由此得切线
,由此得切线![]() 的方程为:
的方程为: ![]() .
.
(Ⅱ)由(Ⅰ)得,直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() .设新的函数
.设新的函数![]() ,
, ![]() 求导,求最值即可.
求导,求最值即可.
(Ⅲ)过![]() 作
作![]() 轴的垂线,与射线
轴的垂线,与射线![]() 交于点
交于点![]() ,得到△
,得到△![]() 是等腰直角三角形,
是等腰直角三角形, ![]() .设
.设 ![]() ,
, ![]() 求最值即可.
求最值即可.
试题解析:
(Ⅰ) 对![]() 求导数,得
求导数,得![]() , 所以切线
, 所以切线![]() 的斜率为
的斜率为![]() ,由此得切线
,由此得切线![]() 的方程为:
的方程为: ![]() , 即
, 即 ![]() .
.
(Ⅱ) 由(Ⅰ)得,直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() .
.
设 ![]() ,
, ![]() .所以
.所以 ![]() ,令
,令![]() ,得
,得![]() .
.
![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
| ||
|
| ↘ |
| ↘ |
|
所以函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
, ![]() ,
,
所以直线![]() 在
在![]() 轴上的截距的取值范围是
轴上的截距的取值范围是![]() .
.
(Ⅲ)过![]() 作
作![]() 轴的垂线,与射线
轴的垂线,与射线![]() 交于点
交于点![]() ,
,
所以△![]() 是等腰直角三角形.所以
是等腰直角三角形.所以 ![]() .
.
设 ![]() ,
, ![]() ,
,
所以 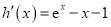 .
.
令 ![]() ,则
,则![]() ,
,
所以 ![]() 在
在![]() 上单调递增,
上单调递增,
所以 ![]() ,
,
从而 ![]() 在
在![]() 上单调递增,所以
上单调递增,所以 ![]() ,此时
,此时![]() ,
, ![]() .
.
所以 ![]() 的最小值为
的最小值为![]() ,此时
,此时![]() .
.
点晴:本题主要考查导数与切线,导数与最值问题. 解答此类问题,应该首先确定函数的定义域,第二问中利用导数把直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() .设新的函数
.设新的函数![]() ,
, ![]() 求导,求最值即可;第三问中借助几何关系
求导,求最值即可;第三问中借助几何关系![]() .得到
.得到 ![]() ,
, ![]() 求最值即可.
求最值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为
 .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.方案乙:员工连续三次抽奖,每次中奖率均为
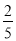 ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.(1)求某员工选择方案甲进行抽奖所获奖金
 (元)的分布列;
(元)的分布列;(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司租赁甲、乙两种设备生产
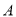 ,
, 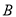 两类产品,甲种设备每天能生产
两类产品,甲种设备每天能生产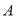 类产品5件和
类产品5件和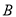 类产品10件,乙种设备每天能生产
类产品10件,乙种设备每天能生产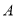 类产品6件和
类产品6件和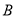 类产品20件.已知设备甲每天的租赁费为300元,设备乙每天的租赁费为400元,现该公司至少要生产
类产品20件.已知设备甲每天的租赁费为300元,设备乙每天的租赁费为400元,现该公司至少要生产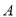 类产品50件,
类产品50件, 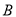 类产品140件,则所需租赁费最少为__________元.
类产品140件,则所需租赁费最少为__________元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
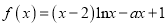 .
.(1)若
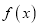 在区间
在区间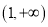 上单调递增,求实数
上单调递增,求实数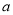 的取值范围;
的取值范围;(2)若存在唯一整数
 ,使得
,使得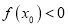 成立,求实数
成立,求实数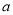 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在测试中,客观题难度的计算公式为
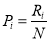 ,其中
,其中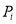 为第
为第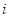 题的难度,
题的难度, 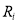 为答对该题的人数,
为答对该题的人数, 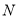 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:题号
1
2
3
4
5
考前预估难度
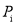
0.9
0.8
0.7
0.6
0.4
测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
 学生编号 题号
学生编号 题号 1
2
3
4
5
1
×
√
√
√
√
2
√
√
√
√
×
3
√
√
√
√
×
4
√
√
√
×
×
5
√
√
√
√
√
6
√
×
×
√
×
7
×
√
√
√
×
8
√
×
×
×
×
9
√
√
×
×
×
10
√
√
√
√
×
(Ⅰ)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;
题号
1
2
3
4
5
实测答对人数
实测难度
(Ⅱ)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(Ⅲ)定义统计量
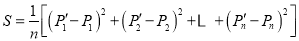 ,其中
,其中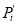 为第
为第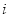 题的实测难度,
题的实测难度, 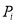 为第
为第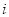 题的预估难度
题的预估难度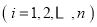 .规定:若
.规定:若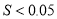 ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理. -
科目: 来源: 题型:
查看答案和解析>>【题目】张师傅想要一个如图1所示的钢筋支架的组合体,来到一家钢制品加工店定制,拿出自己画的组合体三视图(如图2所示).店老板看了三视图,报了最低价,张师傅觉得很便宜,当即甩下定金和三视图,约定第二天提货.第二天提货时,店老板一脸坏笑的捧出如图3–1所示的组合体,张师傅一看,脸都绿了:“奸商,怎能如此偷工减料”.店老板说,我是按你的三视图做的,要不我给你加一个正方体,但要加价,随机加上了一个正方体,得到如图3–2所示的组合体;张师傅脸还是绿的,店老板又加上一个正方体,组成了如图 3–3 所示的组合体,又加价;张师傅脸继续绿,店老板再加一个正方体,组成如图 3–4 所示的组合体,再次加价;双方就三视图争吵不休……
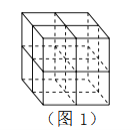
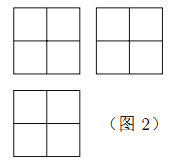
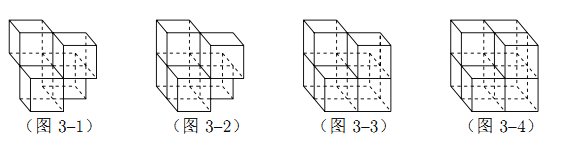
你认为店老板提供的
 个组合体的三视图与张师傅画的三视图一致的个数是( )
个组合体的三视图与张师傅画的三视图一致的个数是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
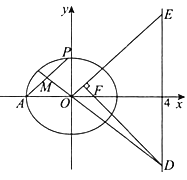
查看答案和解析>>【题目】如图,已知椭圆
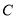 :
: 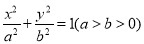 的离心率为
的离心率为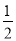 ,
, 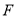 为椭圆
为椭圆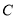 的右焦点,
的右焦点, 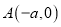 ,
, 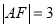 .
.
(Ⅰ)求椭圆
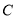 的方程;
的方程;(Ⅱ)设
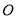 为原点,
为原点, 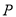 为椭圆上一点,
为椭圆上一点, 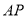 的中点为
的中点为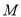 ,直线
,直线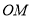 与直线
与直线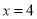 交于点
交于点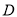 ,过
,过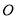 作
作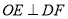 ,交直线
,交直线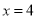 于点
于点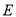 ,求证:
,求证: 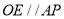 .
.
相关试题

