【题目】已知函数![]() 函数在点
函数在点![]() 处的切线为
处的切线为![]() .
.
(1)求函数![]() 的值,并求出
的值,并求出![]() 在
在![]() 上的单调区间;
上的单调区间;
(2)若![]() ,且
,且![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)![]() 时,
时,![]() 为增函数,
为增函数,![]() 时,
时,![]() 为减函数;(2)证明见解析.
为减函数;(2)证明见解析.
【解析】
试题分析:(1)先利用切点和斜率,列方程组,求得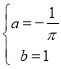 ,此时
,此时![]() ,将区间分为
,将区间分为![]() 和
和![]() 来研究函数的单调性,其中
来研究函数的单调性,其中![]() 部分要用二阶导数来求;(2)根据
部分要用二阶导数来求;(2)根据![]() ,代入函数的表达式,化简得
,代入函数的表达式,化简得![]() ,令
,令![]() ,换元后构造函数
,换元后构造函数![]() ,利用导数证明,
,利用导数证明,![]() .
.
试题解析:
(1)由题意:![]() ,所以
,所以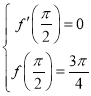 ,解得
,解得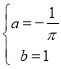 ,
,
故![]() ..................2分
..................2分
当![]() 时,
时,![]() 为减函数,且
为减函数,且![]() 为增函数,.................3分
为增函数,.................3分
当![]() 时,
时,![]() 为增函数,且
为增函数,且![]() ,
,
故存在唯一![]() 使
使![]() ,所以
,所以![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
又因为![]() ,所以
,所以![]() 时,
时,![]() 为减函数,............5分
为减函数,............5分
综上可知:![]() 时,
时,![]() 为增函数;
为增函数;
![]() 时,
时,![]() 为减函数.........................6分
为减函数.........................6分
(2)由![]() ,得
,得![]() ,
,
所以![]() ,两边同除以
,两边同除以![]() ,
,
得![]() ,令
,令![]() ,则
,则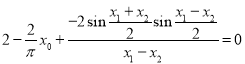 ,
,
所以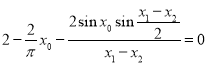 ,得
,得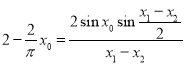 ......8分
......8分
因为![]() ,所以
,所以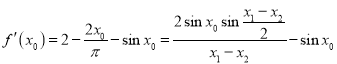
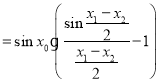 .............................9分
.............................9分
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 为减函数,
为减函数,
当![]() 时,
时,![]() 为减函数,........................11分
为减函数,........................11分
所以![]() ,(也可以利用斜率),所以
,(也可以利用斜率),所以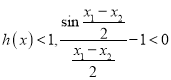 ,
,
又![]() ,所以
,所以![]() ,故
,故![]() ,........................12分
,........................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面几种推理是合情推理的是 ( )
①由圆的性质类比出球的有关性质
②由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180°
③某次考试张军成绩是100分,由此推出全班同学成绩都是100分
④数列1,0,1,0,…,推测出每项公式
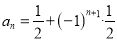
A. ①② B. ①③④ C. ①②④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的年销售量
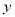 与该年广告费用支出
与该年广告费用支出 有关,现收集了4组观测数据列于下表:
有关,现收集了4组观测数据列于下表: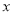 (万元)
(万元)1
4
5
6
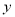 (万元)
(万元)30
40
60
50
现确定以广告费用支出
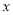 为解释变量,销售量
为解释变量,销售量 为预报变量对这两个变量进行统计分析.
为预报变量对这两个变量进行统计分析.(1)已知这两个变量满足线性相关关系,试建立
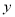 与
与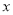 之间的回归方程;
之间的回归方程;(2)假如2017年广告费用支出为10万元,请根据你得到的模型,预测该年的销售量
 .
.(线性回归方程系数公式
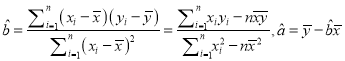 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
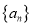 满足
满足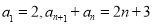 .
.(1)求
 ;
;(2)求
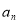 的表达式.
的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我海监船在
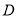 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至 处,此时测得其东北方向与它相距32海里的
处,此时测得其东北方向与它相距32海里的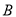 处有一外国船只,且
处有一外国船只,且 岛位于海监船正东
岛位于海监船正东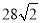 海里处.
海里处.
(1)求此时该外国船只与
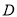 岛的距离;
岛的距离;(2)观测中发现,此外国船只正以每小时8海里的速度沿正南方向航行,为了将该船拦截在离
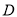 岛24海里处,不让其进入
岛24海里处,不让其进入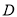 岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据: 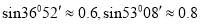 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一项针对人们休闲方式的调查结果如下:受调查对象总计124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个
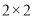 的列联表;
的列联表;(2)根据下列提供的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?
独立检验临界值表:
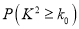
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
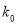
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:
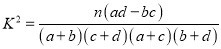 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前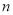 项和为
项和为 ,且满足
,且满足 .
.(1)求证:数列
 为等比数列;
为等比数列;(2)若
 ,求
,求 的前
的前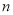 项和
项和 .
.
相关试题

