【题目】设f(logax)= ![]() ,(0<a<1)
,(0<a<1)
(1)求f(x)的表达式,并判断f(x)的奇偶性;
(2)判断f(x)的单调性;
(3)对于f(x),当x∈(﹣1,1)时,恒有f(1﹣m)+f(1﹣m2)<0,求m的取值范围.
参考答案:
【答案】
(1)解:设logax=t,则x=at,
∴f(t)= ![]() =
= ![]() =
= ![]()
∴f(x)= ![]()
∴f(﹣x)= ![]() (a﹣x﹣ax)=﹣f(x),
(a﹣x﹣ax)=﹣f(x),
∴f(x)为奇函数
(2)解:函数为增函数,
∵f(x)= ![]()
设x1<x2,f(x1)﹣f(x2)= ![]() (
( ![]() )=
)= ![]() (
( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() ),
),
∵0<a<1时,
∴a2﹣1<0, ![]() >1,
>1,
∴ ![]() ﹣
﹣ ![]() >0,+
>0,+ ![]() ﹣
﹣ ![]() >0,
>0,
∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),
∴f(x)在(﹣∞,+∞)上单调递增
(3)解:∵f(1﹣m)+f(1﹣m2)<0,
∴f(1﹣m)<﹣f(1﹣m2)=f(m2﹣1),
∵f(x)在(﹣∞,+∞)上单调递增;
∴ 
解得,1<m ![]() ,
,
故m的取值范围为(1, ![]() )
)
【解析】(1)利用换元法,设logax=t,则x=at , 代入化简即可,再利用奇偶性的定义证明即可,(2)函数为增函数,利用定义证明即可,(3)利用函数为奇函数和增函数,得到不等式组,解得即可.
【考点精析】关于本题考查的函数的奇偶性和利用导数研究函数的单调性,需要了解偶函数的图象关于y轴对称;奇函数的图象关于原点对称;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A={x|x2-ax+a2-19=0},B={ x|x2-5x+6=0},C={x|x2+2x-8=0},且

 (A∩B),A∩C=
(A∩B),A∩C= ,求
,求 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是等腰梯形,
是等腰梯形, 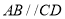 ,
, 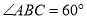 ,
, 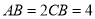 ,在梯形
,在梯形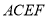 中,
中, 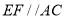 ,且
,且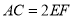 ,
, 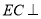 平面
平面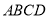 .
.(1)求证:面
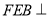 面
面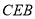 ;
;(2)若二面角
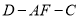 的大小为
的大小为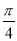 ,求几何体
,求几何体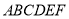 的体积.
的体积.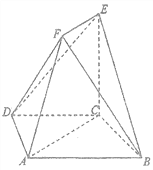
-
科目: 来源: 题型:
查看答案和解析>>【题目】备受瞩目的巴西世界杯正在如火如荼的进行,为确保总决赛的顺利进行,组委会决定在位于里约热内卢的马拉卡纳体育场外临时围建一个矩形观众候场区,总面积为72m2(如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为2m的入口.现已知铁栏杆的租用费用为100元/m.设该矩形区域的长为x(单位:m),租用铁栏杆的总费用为y(单位:元)
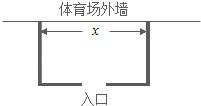
(1)将y表示为x的函数;
(2)试确定x,使得租用此区域所用铁栏杆所需费用最小,并求出最小最小费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣mx+m,m∈R.
(1)已知函数f(x)在点(l,f(1))处与x轴相切,求实数m的值;
(2)求函数f(x)的单调区间;
(3)在(1)的结论下,对于任意的0<a<b,证明: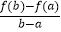 <
< 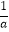 ﹣1.
﹣1. -
科目: 来源: 题型:
查看答案和解析>>【题目】从椭圆
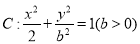 上一点
上一点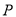 向
向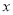 轴作垂线,垂足恰好为椭圆的左焦点
轴作垂线,垂足恰好为椭圆的左焦点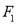 ,
,  是椭圆的右顶点,
是椭圆的右顶点, 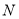 是椭圆的上顶点,且
是椭圆的上顶点,且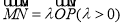 .
.(1)求该椭圆
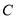 的方程;
的方程;(2)不过原点的直线
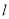 与椭圆
与椭圆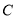 交于
交于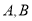 两点,已知
两点,已知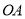 ,直线
,直线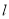 ,
, 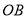 的斜率
的斜率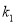 ,
, 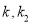 成等比数列,记以
成等比数列,记以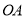 ,
, 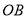 为直径的圆的面积分别为
为直径的圆的面积分别为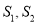 ,求证;
,求证; 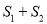 为定值,并求出定值.
为定值,并求出定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
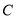 与直线
与直线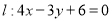 相切于点
相切于点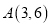 ,且经过点
,且经过点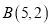 ,求圆
,求圆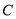 的方程.
的方程.
相关试题

