【题目】如图所示,以原点![]() 为圆心的两个同心圆
为圆心的两个同心圆![]() ,其中,大圆
,其中,大圆![]() 的半径为
的半径为![]() ,小圆的半径为
,小圆的半径为![]() ,点
,点![]() 为大圆
为大圆![]() 上一动点,连接
上一动点,连接![]() ,与小圆
,与小圆![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,点
,点![]() ,记
,记![]() .
.
(1)求点![]() 的坐标(用含有
的坐标(用含有![]() 的式子表示),并写出点
的式子表示),并写出点![]() 的轨迹方程,指出点
的轨迹方程,指出点![]() 的轨迹是什么曲线;
的轨迹是什么曲线;
(2)设点![]() 的轨迹为
的轨迹为![]() ,点
,点![]() 分别是曲线
分别是曲线![]() 上的两个动点,且
上的两个动点,且![]() ,求
,求![]() 的值.
的值.
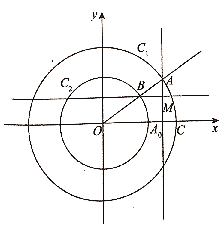
参考答案:
【答案】(1)点![]() 的轨迹方程为
的轨迹方程为![]() ,点
,点![]() 的轨迹是一个中心为原点,焦点在
的轨迹是一个中心为原点,焦点在![]() 轴上的椭圆.(2)
轴上的椭圆.(2)![]()
【解析】试题分析:(1)根据题意可根据极坐标定义得![]() ,化为普通方程即得答案(2)可设
,化为普通方程即得答案(2)可设![]() 其中
其中![]() ,由E,F在椭圆上,代入可得
,由E,F在椭圆上,代入可得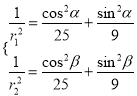 ,再将
,再将![]() 化简表达式即可求解
化简表达式即可求解
试题解析:
解:
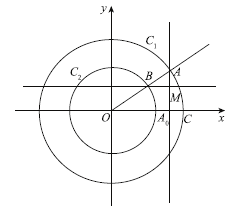
(1)![]() ,则点
,则点![]() 的轨迹方程为
的轨迹方程为![]() ,
,
点![]() 的轨迹是一个中心为原点,焦点在
的轨迹是一个中心为原点,焦点在![]() 轴上的椭圆.
轴上的椭圆.
(2)设![]() ,其中
,其中![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以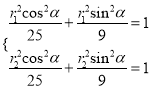 ,所以
,所以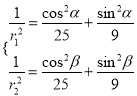 ,
,
则![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分) 函数f(x)是定义在R上的偶函数,已知当x≤0时,f(x)=x2+4x+3.
(1)求函数f(x)的解析式;
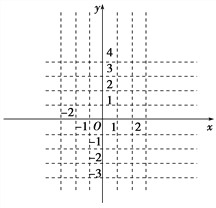
(2)画出函数的图象,并写出函数f(x)的单调区间;
(3)求f(x)在区间[-1,2]上的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)求下列函数的解析式:
(1)已知
 ,求
,求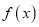 ;
;(2) 已知函数
 是一次函数,且满足关系式
是一次函数,且满足关系式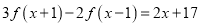 ,求
,求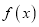 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的短轴长为
的短轴长为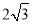 ,离心率
,离心率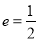 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若
 分别是椭圆
分别是椭圆 的左、右焦点,过
的左、右焦点,过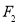 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,求
,求 的内切圆半径的最大值.
的内切圆半径的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
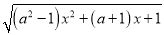 ;
;(1)若f(x)的定义域为 (-∞,+∞), 求实数a的范围;
(2)若f(x)的值域为 [0, +∞), 求实数a的范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知在直角坐标系中,曲线
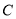 的参数方程为
的参数方程为 (
(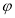 为参数),现以原点为极点,
为参数),现以原点为极点,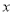 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线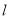 的极坐标方程为
的极坐标方程为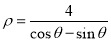 .
.(1)求曲线
 的普通方程和直线
的普通方程和直线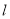 的直角坐标方程;
的直角坐标方程;(2)在曲线
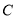 上是否存在一点
上是否存在一点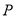 ,使点
,使点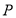 到直线
到直线 的距离最小?若存在,求出距离的最小值及点
的距离最小?若存在,求出距离的最小值及点 的直角坐标;若不存在,请说明理由.
的直角坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ln x+
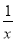 +ax(a是实数),g(x)=
+ax(a是实数),g(x)=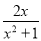 +1.
+1.(1)当a=2时,求函数f(x)在定义域上的最值;
(2)若函数f(x)在[1,+∞)上是单调函数,求a的取值范围;
(3)是否存在正实数a满足:对于任意x1∈[1,2],总存在x2∈[1,2],使得f(x1)=g(x2)成立? 若存在,求出a的取值范围,若不存在,说明理由.
相关试题

