【题目】选修4-4:坐标系与参数方程
已知在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),现以原点为极点,
为参数),现以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上是否存在一点
上是否存在一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最小?若存在,求出距离的最小值及点
的距离最小?若存在,求出距离的最小值及点![]() 的直角坐标;若不存在,请说明理由.
的直角坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
试题分析:(1)把曲线![]() 的参数方程分类参数,根据同角三角函数的基本关系消去参数得到其普通方程,根据
的参数方程分类参数,根据同角三角函数的基本关系消去参数得到其普通方程,根据![]() 把直线的极坐标方程化成直角坐标方程;(2)设
把直线的极坐标方程化成直角坐标方程;(2)设![]() ,由点到直线的距离公式得到距离
,由点到直线的距离公式得到距离![]() 关于参数的
关于参数的![]() 的函数关系,通过三角恒等变换和三角函数的性质得到最小值和相应点的坐标.
的函数关系,通过三角恒等变换和三角函数的性质得到最小值和相应点的坐标.
试题解析:(1)由题意知曲线![]() 的参数方程
的参数方程![]() 可化简为
可化简为![]() ,
,
..................3分
由直线![]() 的极坐标方程可得直角坐标方程为
的极坐标方程可得直角坐标方程为![]() ...................5分
...................5分
(2)若点![]() 是曲线
是曲线![]() 上任意一点,则可设
上任意一点,则可设![]() ,
,
设其到直线![]() 的距离为
的距离为![]() ,则
,则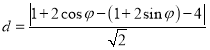 ..............7分
..............7分
化简得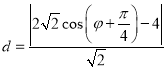 ,当
,当![]() ,即
,即![]() 时,
时,![]() ......................9分
......................9分
此时点![]() 的坐标为
的坐标为![]() ……………………10分
……………………10分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的短轴长为
的短轴长为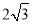 ,离心率
,离心率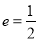 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若
 分别是椭圆
分别是椭圆 的左、右焦点,过
的左、右焦点,过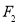 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,求
,求 的内切圆半径的最大值.
的内切圆半径的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,以原点
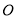 为圆心的两个同心圆
为圆心的两个同心圆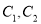 ,其中,大圆
,其中,大圆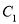 的半径为
的半径为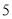 ,小圆的半径为
,小圆的半径为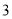 ,点
,点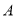 为大圆
为大圆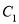 上一动点,连接
上一动点,连接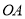 ,与小圆
,与小圆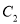 交于点
交于点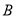 ,过点
,过点 作
作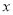 轴的垂线,垂足为
轴的垂线,垂足为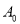 ,过点
,过点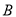 作直线
作直线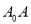 的垂线,垂足为
的垂线,垂足为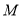 ,点
,点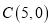 ,记
,记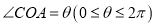 .
.(1)求点
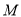 的坐标(用含有
的坐标(用含有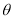 的式子表示),并写出点
的式子表示),并写出点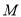 的轨迹方程,指出点
的轨迹方程,指出点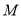 的轨迹是什么曲线;
的轨迹是什么曲线;(2)设点
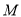 的轨迹为
的轨迹为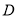 ,点
,点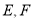 分别是曲线
分别是曲线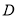 上的两个动点,且
上的两个动点,且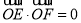 ,求
,求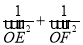 的值.
的值.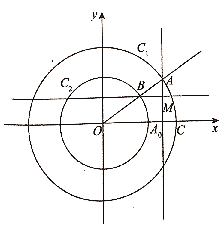
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
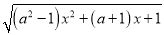 ;
;(1)若f(x)的定义域为 (-∞,+∞), 求实数a的范围;
(2)若f(x)的值域为 [0, +∞), 求实数a的范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ln x+
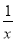 +ax(a是实数),g(x)=
+ax(a是实数),g(x)=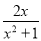 +1.
+1.(1)当a=2时,求函数f(x)在定义域上的最值;
(2)若函数f(x)在[1,+∞)上是单调函数,求a的取值范围;
(3)是否存在正实数a满足:对于任意x1∈[1,2],总存在x2∈[1,2],使得f(x1)=g(x2)成立? 若存在,求出a的取值范围,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年5月,我省南昌市遭受连日大暴雨天气,某网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票,按照南昌暴雨前后两个时间收集有效投票,暴雨后的投票收集了
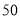 份,暴雨前的投票也收集了
份,暴雨前的投票也收集了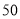 份,所得统计结果如下表:
份,所得统计结果如下表:
已知工作人与从所有投票中任取一个,取到“不支持投入”的投票的概率为
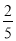 .
.(1)求列表中数据的值;
(2)能够有多大的把握认为南昌暴雨对民众是否赞成加大对修建城市地下排水设施的投入有关系?
附:
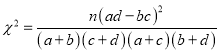
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳
不喜欢游泳
合计
男生
10
女生
20
合计
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为
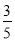 .
.(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
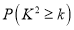
0.15
0.10
0.05
0.025
0.010
0.005
0.001
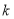
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:
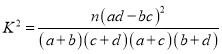 ,其中
,其中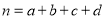 )
)
相关试题

