【题目】已知函数f(x)=lnx﹣mx+m,m∈R.
(1)求函数f(x)的单调区间.
(2)若f(x)≤0在x∈(0,+∞)上恒成立,求实数m的取值范围.
(3)在(2)的条件下,任意的0<a<b, ![]() .
.
参考答案:
【答案】
(1)
解: ![]()
当m≤0时,f′(x)>0恒成立,则函数f(x)在(0,+∞)上单调递增;
当m>0时,由 ![]()
则 ![]() ,则f(x)在
,则f(x)在 ![]() 上单调递增,在
上单调递增,在 ![]() 上单调递减.
上单调递减.
(2)
解:由(1)得:当m≤0时显然不成立;
当m>0时, ![]() 只需m﹣lnm﹣1≤0即
只需m﹣lnm﹣1≤0即
令g(x)=x﹣lnx﹣1,
则 ![]() ,函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增.∴g(x)min=g(1)=0.则若f(x)≤0在x∈(0,+∞)上恒成立,m=1.
,函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增.∴g(x)min=g(1)=0.则若f(x)≤0在x∈(0,+∞)上恒成立,m=1.
(3)
解: 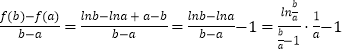
由0<a<b得 ![]() ,
,
由(2)得: ![]() ,则
,则  ,
,
则原不等式 ![]() 成立.
成立.
【解析】(1)求函数f(x)的单调区间,可先求 ![]() ,再解出函数的单调区间;(2)若f(x)≤0在x∈(0,+∞)上恒成立,可利用导数研究函数的单调性确定出函数的最大值,令最大值小于等于0,即可得到关于m的不等式,解出m的取值范围;(3)在(2)的条件下,任意的0<a<b,可先代入函数的解析式,得出
,再解出函数的单调区间;(2)若f(x)≤0在x∈(0,+∞)上恒成立,可利用导数研究函数的单调性确定出函数的最大值,令最大值小于等于0,即可得到关于m的不等式,解出m的取值范围;(3)在(2)的条件下,任意的0<a<b,可先代入函数的解析式,得出 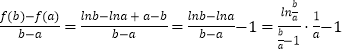 再由0<a<b得出
再由0<a<b得出 ![]() ,代入即可证明出不等式.
,代入即可证明出不等式.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,点
中,点 是曲线
是曲线 上的动点,
上的动点,  到点
到点 的距离与
的距离与 到直线
到直线 的距离相等.
的距离相等.(Ⅰ)求曲线
 的方程;
的方程;(Ⅱ)设
 是曲线
是曲线 上的点,点
上的点,点 在曲线
在曲线 上,直线
上,直线 分别与
分别与 轴交于点
轴交于点 ,且
,且 ,求直线
,求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2
 ,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1 .
,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1 . 
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线CD与平面ABC所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.
(1)若p=2且∠BFD=90°时,求圆F的方程;
(2)若A,B,F三点在同一直线m上,设直线m与抛物线C的另一个交点为E,在y轴上求一点G,使得∠OGE=∠OGA. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4﹣1:几何证明选讲
如图,已知四边形ABCD内接于⊙O,且AB是的⊙O直径,过点D的⊙O的切线与BA的延长线交于点M.
(1)若MD=6,MB=12,求AB的长;
(2)若AM=AD,求∠DCB的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用
 表示.(把频率当作概率).
表示.(把频率当作概率).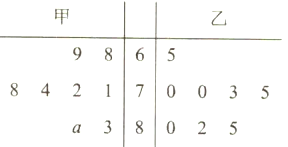
(1)假设
 ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?(2)假设数字
 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:
 (t为参数,α≠0)经过椭圆C:
(t为参数,α≠0)经过椭圆C:  (φ为参数)的左焦点F.
(φ为参数)的左焦点F.
(1)求实数m的值;
(2)设直线l与椭圆C交于A、B两点,求|FA|×|FB|取最小值时,直线l的倾斜角α.
相关试题

