【题目】已知函数f(x)=sin2x﹣ ![]() cos2x
cos2x
(1)求函数的最小正周期及函数图象的对称中心;
(2)若不等式﹣2<f(x)﹣m<2在x∈[ ![]() ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
参考答案:
【答案】
(1)解:f(x)=sin2x﹣ ![]() cos2x=
cos2x= ![]() .
.
函数的周期为T= ![]() .
.
由2x ![]() ,得x=
,得x= ![]() ,
,
∴函数的对称中心为( ![]() ),k∈Z
),k∈Z
(2)解:由﹣2<f(x)﹣m<2在x∈[ ![]() ]上恒成立,
]上恒成立,
得f(x)﹣2<m<f(x)+2在x∈[ ![]() ]上恒成立,
]上恒成立,
∵x∈[ ![]() ],∴2x
],∴2x ![]() ∈[
∈[ ![]() ],则f(x)∈[1,2],
],则f(x)∈[1,2],
∴0<m<3.
∴实数m的取值范围是(0,3)
【解析】利用辅助角公式化积.(1)直接利用周期公式求得周期,再由相位的终边落在x轴上求得函数图象的对称中心;(2)由x得范围求得f(x)的范围,把﹣2<f(x)﹣m<2在x∈[ ![]() ]上恒成立转化为f(x)﹣2<m<f(x)+2在x∈[
]上恒成立转化为f(x)﹣2<m<f(x)+2在x∈[ ![]() ]上恒成立得答案.
]上恒成立得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
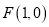 ,动点
,动点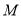 ,
, 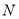 分别在
分别在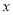 轴,
轴, 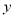 轴上运动,
轴上运动, 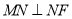 ,
, 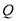 为平面上一点,
为平面上一点, 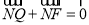 ,过点
,过点 作
作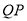 平行于
平行于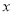 轴交
轴交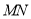 的延长线于点
的延长线于点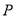 .
.(Ⅰ)求点
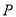 的轨迹曲线
的轨迹曲线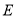 的方程;
的方程;(Ⅱ)过
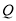 点作
点作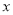 轴的垂线
轴的垂线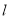 ,平行于
,平行于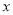 轴的两条直线
轴的两条直线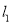 ,
, 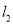 分别交曲线
分别交曲线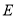 于
于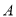 ,
, 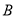 两点(直线
两点(直线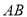 不过
不过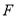 ),交
),交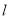 于
于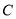 ,
, 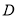 两点.若线段
两点.若线段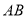 中点的轨迹方程为
中点的轨迹方程为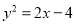 ,求
,求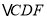 与
与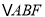 的面积之比.
的面积之比.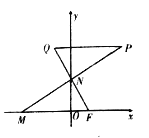
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:函数f(x)=Asin(ωx+)(A>0,ω>0,||<
 )的部分图象如图所示:
)的部分图象如图所示: 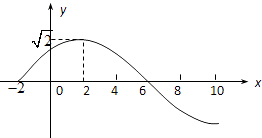
(1)求函数f(x)的解析式;
(2)若g(x)的图象是将f(x)的图象先向右平移1个单位,然后纵坐标不变横坐标缩短到原来的一半得到的,求g(x)的单调递增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】潮州统计局就某地居民的月收入调查了
 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在
 )。
)。
(1)求居民月收入在
 的频率;
的频率;(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这
 人中分层抽样方法抽出
人中分层抽样方法抽出 人作进一步分析,则月收入在
人作进一步分析,则月收入在 的这段应抽多少人?
的这段应抽多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题10分) 从3名男生和
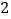 名女生中任选2人参加比赛。
名女生中任选2人参加比赛。①求所选2人都是男生的概率;
②求所选2人恰有1名女生的概率;
③求所选2人中至少有1名女生的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
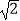 sin(2x+
sin(2x+  ),给出下列四个命题:
),给出下列四个命题:
①函数f(x)在区间[ ,
, 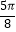 ]上是减函数;
]上是减函数;
②直线x= 是f(x)的图象的一条对称轴;
是f(x)的图象的一条对称轴;
③函数f(x)的图象可以由函数y=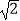 sin2x的图象向左平移
sin2x的图象向左平移  而得到;
而得到;
④函数f(x)的图象的一个对称中心是(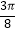 ,0).
,0).
其中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①在△ABC中,若A<B,则sinA<sinB;
②在同一坐标系中,函数y=sinx与y=lgx的交点个数为2个;
③函数y=|tan2x|的最小正周期为 ;
;
④存在实数x,使2sin(2x﹣ )﹣1=
)﹣1=  成立;
成立;
其中正确的命题为(写出所有正确命题的序号).
相关试题

