【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
参考答案:
【答案】(1)0.15;(2)2400;(3)25.
【解析】试题分析:(1)根据频率=小矩形的高×组距来求;(2)根据中位数的左右两边的矩形的面积和相等,所以只需求出从左开始面积和等于0.5的底边横坐标的值即可,运用取中间数乘频率,再求之和,计算可得平均数;(3)求出月收入在[2500,3000)的人数,用分层抽样的抽取比例乘以人数,可得答案.
试题解析:
(1)月收入在![]() 的频率为
的频率为![]() ;
;
(2)从左数第一组的频率为![]() ;
;
第二组的频率为![]() ;
;
第三组的频率为![]() ;
;
∴中位数在第三组,设中位数为![]()
则![]()
得![]()
∴中位数为2400(元)
由![]()
样本的平均数为2400(元)
(3)月收入在![]() 的频数为
的频数为![]() (人),
(人),
∵抽取的样本容量为100,∴抽取的比例为![]() ,
,
∴月收入在![]() 的这段应抽取为
的这段应抽取为![]() (人)
(人)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 简单随机抽样每个个体被抽到的机会不一样,与先后有关
B. 由生物学知道生男生女的概率均为
 ,一对夫妇生两个孩子,则一定为一男一女
,一对夫妇生两个孩子,则一定为一男一女C. 互斥事件一定是对立事件,对立事件不一定是互斥事件
D. 老师在某班学号为1~50的50名学生中依次抽取学号为5,10,15,20,25,30,35,40,45,50的学生进行作业检查,这种抽样方法是系统抽样
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
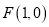 ,动点
,动点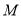 ,
, 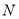 分别在
分别在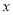 轴,
轴, 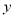 轴上运动,
轴上运动, 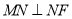 ,
, 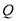 为平面上一点,
为平面上一点, 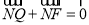 ,过点
,过点 作
作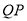 平行于
平行于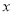 轴交
轴交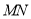 的延长线于点
的延长线于点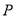 .
.(Ⅰ)求点
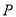 的轨迹曲线
的轨迹曲线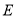 的方程;
的方程;(Ⅱ)过
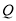 点作
点作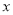 轴的垂线
轴的垂线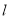 ,平行于
,平行于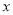 轴的两条直线
轴的两条直线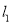 ,
, 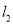 分别交曲线
分别交曲线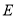 于
于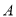 ,
, 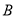 两点(直线
两点(直线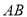 不过
不过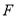 ),交
),交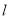 于
于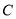 ,
, 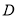 两点.若线段
两点.若线段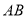 中点的轨迹方程为
中点的轨迹方程为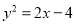 ,求
,求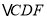 与
与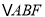 的面积之比.
的面积之比.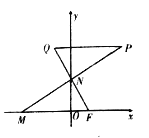
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:函数f(x)=Asin(ωx+)(A>0,ω>0,||<
 )的部分图象如图所示:
)的部分图象如图所示: 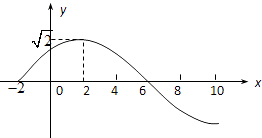
(1)求函数f(x)的解析式;
(2)若g(x)的图象是将f(x)的图象先向右平移1个单位,然后纵坐标不变横坐标缩短到原来的一半得到的,求g(x)的单调递增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin2x﹣
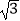 cos2x
cos2x
(1)求函数的最小正周期及函数图象的对称中心;
(2)若不等式﹣2<f(x)﹣m<2在x∈[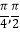 ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题10分) 从3名男生和
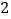 名女生中任选2人参加比赛。
名女生中任选2人参加比赛。①求所选2人都是男生的概率;
②求所选2人恰有1名女生的概率;
③求所选2人中至少有1名女生的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
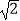 sin(2x+
sin(2x+  ),给出下列四个命题:
),给出下列四个命题:
①函数f(x)在区间[ ,
, 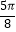 ]上是减函数;
]上是减函数;
②直线x= 是f(x)的图象的一条对称轴;
是f(x)的图象的一条对称轴;
③函数f(x)的图象可以由函数y=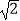 sin2x的图象向左平移
sin2x的图象向左平移  而得到;
而得到;
④函数f(x)的图象的一个对称中心是(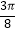 ,0).
,0).
其中正确的个数是( )
A.1
B.2
C.3
D.4
相关试题

