【题目】已知函数 ![]() 是偶函数,g(x)=t2x+4,
是偶函数,g(x)=t2x+4,
(1)求a的值;
(2)当t=﹣2时,求f(x)<g(x)的解集;
(3)若函数f(x)的图象总在g(x)的图象上方,求实数t的取值范围.
参考答案:
【答案】
(1)解:由f(x)是偶函数,得f(x)=f(﹣x),即 ![]() ,
,
化简得22ax=4x,故a=1
(2)解:f(x)<g(x)即 ![]() ,亦即34x﹣42x+1<0,
,亦即34x﹣42x+1<0,
所以 ![]() ,即
,即 ![]() ,
,
所以不等式f(x)<g(x)的解集为 ![]()
(3)解:因为函数f(x)的图象总在g(x)的图象上方,
所以f(x)>g(x),即 ![]() ,得
,得 ![]() ,
,
∵ ![]() ,∴t<﹣3;
,∴t<﹣3;
故实数t的取值范围为:t<﹣3
【解析】(1)由偶函数的定义知f(x)=f(﹣x),化简即可求得a值;(2)对f(x)<g(x)进行等价变形可化为关于2x的二次不等式,解得2x的范围,进而可得x的范围;(3)函数f(x)的图象总在g(x)的图象上方,等价于f(x)>g(x)恒成立,分离出t后转化为求函数的最值解决;
【考点精析】本题主要考查了函数单调性的性质和复合函数单调性的判断方法的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准
 (吨),用水量不超过
(吨),用水量不超过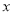 的部分按平价收费,超过
的部分按平价收费,超过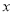 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照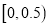 ,
, 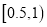 ,…,
,…, 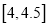 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.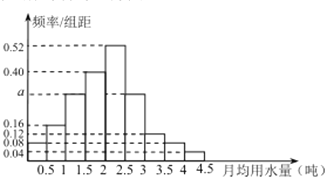
(Ⅰ)求直方图中
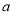 的值;
的值;(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使
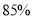 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准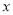 (吨),估计
(吨),估计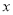 的值,并说明理由;
的值,并说明理由; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+mx+n有两个零点﹣1与3.
(1)求出函数f(x)的解析式,并指出函数f(x)的单调递增区间;
(2)若g(x)=f(|x|)在x1 , x2∈[t,t+1]是增函数,求实数t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列
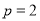 中,已知
中,已知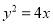 对任意
对任意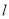 都成立,数列
都成立,数列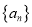 的前
的前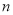 项和为
项和为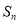 .(这里
.(这里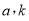 均为实数)
均为实数)(1)若
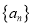 是等差数列,求
是等差数列,求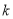 的值;
的值;(2)若
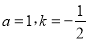 ,求
,求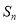 ;
;(3)是否存在实数
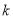 ,使数列
,使数列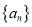 是公比不为
是公比不为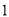 的等比数列,且任意相邻三项
的等比数列,且任意相邻三项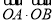 按某顺序排列后成等差数列?若存在,求出所有
按某顺序排列后成等差数列?若存在,求出所有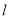 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名射手在一次射击中的得分是两个随机变量,分别记为X和Y,它们的分布列分别为
X
0
1
2
P
0.1
a
0.4
Y
0
1
2
P
0.2
0.2
b
(1)求a,b的值;
(2)计算X和Y的期望与方差,并以此分析甲、乙两射手的技术情况. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:方程
 =1所表示的图形是焦点在y轴上的双曲线,命题q:复数z=(m﹣3)+(m﹣1)i对应的点在第二象限,又p或q为真,p且q为假,求实数m的取值范围.
=1所表示的图形是焦点在y轴上的双曲线,命题q:复数z=(m﹣3)+(m﹣1)i对应的点在第二象限,又p或q为真,p且q为假,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于定义域为I的函数y=f(x),如果存在区间[m,n]I,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n],f(x)值域也是[m,n],则称[m,n]是函数y=f(x)的“好区间”.
(1)设g(x)=loga(ax﹣2a)+loga(ax﹣3a)(其中a>0且a≠1),求g(x)的定义域并判断其单调性;
(2)试判断(1)中的g(x)是否存在“好区间”,并说明理由;
(3)已知函数P(x)=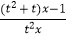 (t∈R,t≠0)有“好区间”[m,n],当t变化时,求n﹣m 的最大值.
(t∈R,t≠0)有“好区间”[m,n],当t变化时,求n﹣m 的最大值.
相关试题

