【题目】设等差数列![]() 的公差
的公差![]() ,且
,且![]() ,记
,记![]()
(1)用![]() 分别表示
分别表示![]() ,并猜想
,并猜想![]() ;
;
(2)用数学归纳法证明你的猜想.
参考答案:
【答案】(1)![]() .;(2)见解析.
.;(2)见解析.
【解析】试题分析:(1)分别求出![]() 的值,观察共有性质,从而可归纳猜想出
的值,观察共有性质,从而可归纳猜想出![]() ;
;
(2)根据数学归纳法的基本原理,①当n=1时,验证猜想正确,②假设当n=k时(k∈N*)时结论成立,证明当n=k+1时结论正确即可.
试题解析:(1)T1=![]() =
=![]() ;
;
T2=![]() +
+![]() =
=![]() ×
×![]() =
=![]() ×
×![]() =
=![]() ;
;
T3=![]() +
+![]() +
+![]() =
=![]() ×
×![]() =
=![]() ×
×![]() =
=![]()
由此可猜想Tn=![]() .
.
(2)证明:①当n=1时,T1=![]() ,结论成立.
,结论成立.
②假设当n=k时(k∈N*)时结论成立,
即Tk=![]() .
.
则当n=k+1时,Tk+1=Tk+![]() =
=![]() +
+![]() =
=![]() =
=![]() .
.
即n=k+1时,结论成立.
由①②可知,Tn=![]() 对于一切n∈N*恒成立.
对于一切n∈N*恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三点A(-1,1,2),B(1,2,-1),C(a,0,3),是否存在实数a,使A、B、C共线?若存在,求出a的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
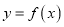 的导函数的图象如图所示,给出下列判断:
的导函数的图象如图所示,给出下列判断:①函数
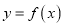 在区间
在区间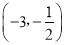 内单调递增;②函数
内单调递增;②函数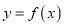 在区间
在区间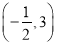 内单调递减;③函数
内单调递减;③函数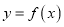 在区间
在区间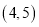 内单调递增;④当
内单调递增;④当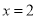 时,函数
时,函数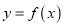 有极小值;⑤当
有极小值;⑤当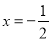 时,函数
时,函数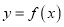 有极大值.则上述判断中正确的是( )
有极大值.则上述判断中正确的是( )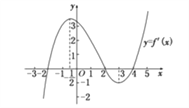
A. ①② B. ③
C. ②③ D. ③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是半圆
是半圆 的直径,
的直径, ,
, 是将半圆圆周四等分的三个分点.
是将半圆圆周四等分的三个分点.
(1)从
 这5个点中任取3个点,求这3个点组成直角三角形的概率;
这5个点中任取3个点,求这3个点组成直角三角形的概率;(2)在半圆内任取一点
 ,求
,求 的面积大于
的面积大于 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥
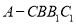 的底面为矩形,D为
的底面为矩形,D为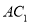
的中点,AC⊥平面BCC1B1.
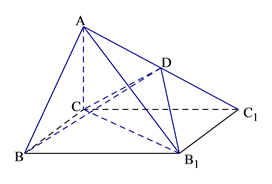
(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=
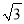 ,
,(1)求BD的长;
(2)求三棱锥C-DB1C1的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2014全国1理21】设函数
 ,曲线
,曲线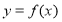 在点
在点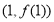 处的切线方程为
处的切线方程为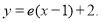
(I)求
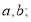
(II)证明:
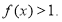
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由9名高二级学生和6名高一级学生组成,现采用分层抽样的方法抽取5人,组成一个体验小组去市场体验“共享单车”的使用.问:
(Ⅰ)应从该兴趣小组中抽取高一级和高二级的学生各多少人;
(Ⅱ)已知该地区有
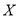 ,
,  两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租
两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租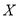 型车,高一级学生都租
型车,高一级学生都租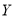 型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租
型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租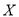 型车的概率.
型车的概率.
相关试题

