【题目】已知圆C经过A(3,2)、B(1,6),且圆心在直线y=2x上. (Ⅰ)求圆C的方程.
(Ⅱ)若直线l经过点P(﹣1,3)与圆C相切,求直线l的方程.
参考答案:
【答案】解:(Ⅰ)∵圆心在直线y=2x上, 故可设圆心C(a,2a),半径为r.
则圆C的标准方程为(x﹣a)2+(y﹣2a)2=r2 .
∵圆C经过A(3,2)、B(1,6),
∴ 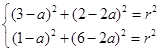 .
.
解得a=2,r= ![]() .
.
∴圆C的标准方程为
(x﹣2)2+(y﹣4)2=5.
(Ⅱ)由(Ⅰ)知,圆C的圆心为C(2,4),半径r= ![]() .
.
直线l经过点P(﹣1,3),
①若直线斜率不存在,
则直线l:x=﹣1.
圆心C(2,4)到直线l的距离为
d=3<r= ![]() ,故直线与圆相交,不符合题意.
,故直线与圆相交,不符合题意.
②若直线斜率存在,设斜率为k,
则直线l:y﹣3=k(x+1),
即kx﹣y+k+3=0.
圆心C(2,4)到直线l的距离为
d= ![]() =
= ![]() .
.
∵直线与圆相切,
∴d=r,即 ![]() =
= ![]() .
.
∴(3k﹣1)2=5+5k2 ,
解得k=2或k= ![]() .
.
∴直线l的方程为2x﹣y+5=0或x+2y﹣5=0
【解析】(Ⅰ)根据已知设出圆的标准方程,将点A,B的坐标代入标准方程,解方程组即可求出圆心及半径,从而得到圆C的方程. (Ⅱ)根据已知设出直线方程,利用直线与圆相切的性质d=r即可求出直线斜率k,从而求出直线方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为一简单组合体,其底面 ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.

(1)求证:BE∥平面PDA;
(2)求四棱锥B﹣CEPD的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
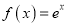 ,直线
,直线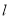 的方程为
的方程为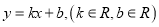 .
.(1)若直线
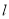 是曲线
是曲线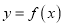 的切线,求证:
的切线,求证: 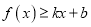 对任意
对任意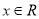 成立;
成立;(2)若
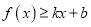 对任意
对任意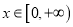 恒成立,求实数是
恒成立,求实数是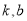 应满足的条件.
应满足的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
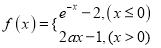 (
(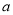 是常数且
是常数且 ),对于下列命题:
),对于下列命题:①函数
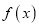 的最小值是
的最小值是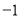 ;
;②函数
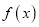 在
在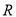 上是单调函数;
上是单调函数;③若
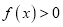 在
在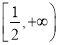 上恒成立,则
上恒成立,则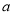 的取值范围是
的取值范围是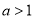 ;
;④对任意的
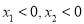 且
且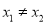 ,恒有
,恒有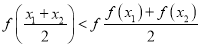
其中正确命题的序号是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
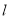 的参数方程为
的参数方程为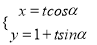 (
(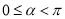 ,
, 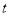 为参数),曲线
为参数),曲线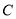 的极坐标方程为
的极坐标方程为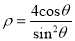 .
.(1)将曲线
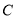 的极坐标方程化为直坐标方程,并说明曲线
的极坐标方程化为直坐标方程,并说明曲线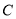 的形状;
的形状;(2)若直线
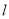 经过点
经过点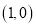 ,求直线
,求直线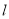 被曲线
被曲线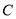 截得的线段
截得的线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( )的图象在
)的图象在 处的切线为
处的切线为 (
( 为自然对数的底数)
为自然对数的底数)(1)求
 的值;
的值;(2)若
 ,且
,且 对任意
对任意 恒成立,求
恒成立,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的外接圆半径R=
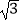 ,角A,B,C的对边分别是a,b,c,且
,角A,B,C的对边分别是a,b,c,且 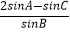 =
= 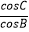
(1)求角B和边长b;
(2)求S△ABC的最大值及取得最大值时的a,c的值,并判断此时三角形的形状.
相关试题

