【题目】某工厂产生的废气经过过滤后排放,排放时污染物的含量不得超过1%.已知在过滤过程中废气中的污染物数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为:P=P0e﹣kt , (k,P0均为正的常数).若在前5个小时的过滤过程中污染物被排除了90%.那么,至少还需( )时间过滤才可以排放.
A.![]() 小时
小时
B.![]() 小时
小时
C.5小时
D.10小时
参考答案:
【答案】C
【解析】解:由题意,前5个小时消除了90%的污染物,
∵P=P0e﹣kt ,
∴(1﹣90%)P0=P0e﹣5k ,
∴0.1=e﹣5k ,
即﹣5k=ln0.1
∴k=﹣ ![]() ln0.1;
ln0.1;
则由10%P0=P0e﹣kt ,
即0.1=e﹣kt ,
∴﹣kt=ln0.1,
即( ![]() ln0.1)t=ln0.1,
ln0.1)t=ln0.1,
∴t=5.
故选:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:
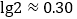 ,
,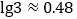 )( )
)( )A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a>0且a≠1,函数y=a2x+2ax﹣1在[﹣1,1]的最大值是14,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,值域是(0,+∞)的是( )
A.y=( )1﹣x
)1﹣x
B.y=x2
C.y=5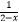
D.y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义域为R的函数f(x)=
 (x)+bf(x)+c=0恰有5个不同的实数解x1 , x2 , x3 , x4 , x5 , 则f(x1+x2+x2+x4+x5)等于 ( )
(x)+bf(x)+c=0恰有5个不同的实数解x1 , x2 , x3 , x4 , x5 , 则f(x1+x2+x2+x4+x5)等于 ( )
A.0
B.21g2
C.31g2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的奇函数
上的奇函数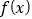 ,设其导函数为
,设其导函数为 ,当
,当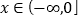 时,恒有
时,恒有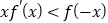 ,令
,令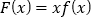 ,则满足
,则满足 的实数
的实数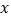 的取值范围是( )
的取值范围是( )A.
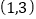 B.
B.  C.
C. 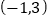 D.
D. 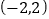
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间生产某种产品,固定成本是
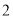 万元,每生产
万元,每生产 件产品成本增加
件产品成本增加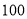 元,根据经验,当年产量少于400件时,总收益
元,根据经验,当年产量少于400件时,总收益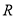 (成本与总利润的和,单位:元)是年产量
(成本与总利润的和,单位:元)是年产量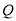 (单位:件)的二次函数;,当年产量不少于
(单位:件)的二次函数;,当年产量不少于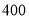 件时,R是Q的一次函数,以下是Q与R的部分数据:
件时,R是Q的一次函数,以下是Q与R的部分数据:Q/ 件
50
200
350
500
650
R/ 元
23750
80000
113750
125000
1332500
问:每年生产多少件产品时,总利润最大?最大利润为多少?
相关试题

