【题目】某车间生产某种产品,固定成本是![]() 万元,每生产
万元,每生产![]() 件产品成本增加
件产品成本增加![]() 元,根据经验,当年产量少于400件时,总收益
元,根据经验,当年产量少于400件时,总收益![]() (成本与总利润的和,单位:元)是年产量
(成本与总利润的和,单位:元)是年产量![]() (单位:件)的二次函数;,当年产量不少于
(单位:件)的二次函数;,当年产量不少于![]() 件时,R是Q的一次函数,以下是Q与R的部分数据:
件时,R是Q的一次函数,以下是Q与R的部分数据:
Q/ 件 | 50 | 200 | 350 | 500 | 650 |
R/ 元 | 23750 | 80000 | 113750 | 125000 | 1332500 |
问:每年生产多少件产品时,总利润最大?最大利润为多少?
参考答案:
【答案】当每年生产400件时利润最大,最大利润为60000元.
【解析】试题分析:根据利润等于收益减去成本,而收益是分段函数,利用待定系数法求对应函数解析式,分别求对应函数最大值,最后取两个最大值中较大值
试题解析: 解:由给定的数据可得总利润与![]() 的关系为:
的关系为:
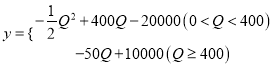
当![]() 时,
时, ![]() 在区间
在区间![]() 为增函数,
为增函数,
当![]() 时,
时, ![]() 在区间
在区间![]() 为减函数,
为减函数,
故当每年生产400件时利润最大,最大利润为60000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂产生的废气经过过滤后排放,排放时污染物的含量不得超过1%.已知在过滤过程中废气中的污染物数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为:P=P0e﹣kt , (k,P0均为正的常数).若在前5个小时的过滤过程中污染物被排除了90%.那么,至少还需( )时间过滤才可以排放.
A. 小时
小时
B. 小时
小时
C.5小时
D.10小时 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义域为R的函数f(x)=
 (x)+bf(x)+c=0恰有5个不同的实数解x1 , x2 , x3 , x4 , x5 , 则f(x1+x2+x2+x4+x5)等于 ( )
(x)+bf(x)+c=0恰有5个不同的实数解x1 , x2 , x3 , x4 , x5 , 则f(x1+x2+x2+x4+x5)等于 ( )
A.0
B.21g2
C.31g2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的奇函数
上的奇函数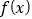 ,设其导函数为
,设其导函数为 ,当
,当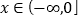 时,恒有
时,恒有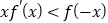 ,令
,令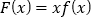 ,则满足
,则满足 的实数
的实数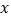 的取值范围是( )
的取值范围是( )A.
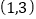 B.
B.  C.
C. 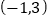 D.
D. 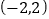
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①原命题为真,它的否命题为假;
②原命题为真,它的 逆命题不一定为真;
③若命题的逆命题为真,则它的否命题一定为真;
④若命题的逆否命题为真,则它的否命题一定为真;
⑤“若 m>1 ,则 mx2-2(m+1)x+m+3>0 的解集为R”的逆命题.
其中真命题是.(把你认为正确命题的序号都填在横线上) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知c>0,设命题p:函数y=cx为减函数.命题q:当
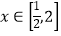 时,函数
时,函数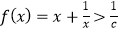 恒成立.如果“p∨q”为真命题,“p∧q”为假命题,求c的取值范围.
恒成立.如果“p∨q”为真命题,“p∧q”为假命题,求c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定点

(1)将极点移至 处极轴方向不变,求P点的新坐标.
处极轴方向不变,求P点的新坐标.
(2)极点不变,将极轴顺时针转动 角,求P点的新坐标.
角,求P点的新坐标.
相关试题

