【题目】电视传媒公司为了了解某地区电视观众对某体育节目的收视情况,随机抽取了100名观众进行调查,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X)
P( K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
参考答案:
【答案】
(1)解:由频率分布直方图可知,在抽取的100人中,“体育迷”有25人,从而2×2列联表如下:
非体育迷 | 体育迷 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
将2×2列联表中的数据代入公式计算,得:
K2= ![]() =
= ![]() ≈3.03,
≈3.03,
因为3.03<3.841,所以没有理由认为“体育迷”与性别有关.
(2)解:由频率分布直方图知抽到“体育迷”的频率是0.25,将频率视为概率,即从观众中抽取到一名“体育迷”的概率是 ![]() ,
,
由题意X∽B(3, ![]() ),从而分布列为
),从而分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以E(X)=np=3× ![]() =
= ![]() .D(X)=npq=3×
.D(X)=npq=3× ![]() ×
× ![]() =
= ![]() .
.
【解析】(1)根据所给的频率分布直方图得出数据列出列联表,再代入公式计算得出K2 , 与3.841比较即可得出结论;(2)由题意,用频率代替概率可得出从观众中抽取到一名“体育迷”的概率是 ![]() ,由于X∽B(3,
,由于X∽B(3, ![]() ),从而给出分布列,再由公式计算出期望与方差即可
),从而给出分布列,再由公式计算出期望与方差即可
【考点精析】利用频率分布直方图对题目进行判断即可得到答案,需要熟知频率分布表频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=ax(a>1),
(1)求函数f(x)的解析式;
(2)若不等式f(x)≤4的解集为[﹣2,2],求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
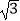 sinxcosx+sin2x﹣
sinxcosx+sin2x﹣  .
.
(1)求f(x)的最小正周期及其对称轴方程;
(2)设函数g(x)=f(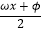 +
+ 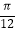 ),其中常数ω>0,|φ|<
),其中常数ω>0,|φ|<  . (i)当ω=4,φ=
. (i)当ω=4,φ=  时,函数y=g(x)﹣4λf(x)在[
时,函数y=g(x)﹣4λf(x)在[ 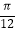 ,
,  ]上的最大值为
]上的最大值为  ,求λ的值;
,求λ的值;
(ii)若函数g(x)的一个单调减区间内有一个零点﹣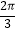 ,且其图象过点A(
,且其图象过点A( 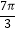 ,1),记函数g(x)的最小正周期为T,试求T取最大值时函数g(x)的解析式.
,1),记函数g(x)的最小正周期为T,试求T取最大值时函数g(x)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.
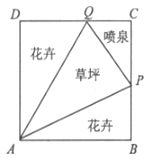
(1)当∠PAQ= 时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
(2)考虑到小区道路的整体规划,要求PB+DQ=PQ,请探究∠PAQ是否为定值,若是,求出此定值,若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥
 ,下部分的形状是正四棱柱
,下部分的形状是正四棱柱 (如图所示),并要求正四棱柱的高
(如图所示),并要求正四棱柱的高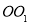 是正四棱锥的高
是正四棱锥的高 的4倍.
的4倍.
(1)若
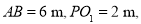 则仓库的容积是多少?
则仓库的容积是多少?(2)若正四棱锥的侧棱长为
 ,则当
,则当 为多少时,仓库的容积最大?
为多少时,仓库的容积最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:日需求量n
14
15
16
17
18
19
20
频数
10
20
16
16
15
13
10
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设偶函数
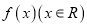 的导函数是函数
的导函数是函数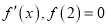 ,当
,当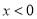 时,
时, 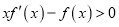 ,则使得
,则使得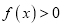 成立的
成立的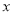 的取值范围是( )
的取值范围是( )A.
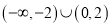 B.
B. 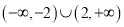
C.
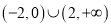 D.
D. 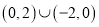
相关试题

