【题目】设函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,讨论
时,讨论![]() 的零点个数.
的零点个数.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ) 求出![]() ,分三种情况讨论,分别令
,分三种情况讨论,分别令 ![]() 得增区间,
得增区间, ![]() 得减区间;(Ⅱ) 由(Ⅰ)知
得减区间;(Ⅱ) 由(Ⅰ)知![]() 在
在![]() 上递增,
上递增, ![]() 上递减,
上递减, ![]() 上递增,利用导数研究函数的单调性,结合零点存在定理,可判定函数在
上递增,利用导数研究函数的单调性,结合零点存在定理,可判定函数在![]() ,
, ![]() ,
, ![]() 上各有一个零点,即可得结果.
上各有一个零点,即可得结果.
试题解析:(Ⅰ) ![]() .
.
①当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() .当
.当![]() 时,
时, ![]() .∴
.∴![]() 在
在![]() 递增
递增
②当![]() 时,令
时,令![]() ,得
,得![]() ,此时
,此时![]() .
.
易知![]() 在
在![]() 递增,
递增, ![]() 递减,
递减, ![]() 递增
递增
③当![]() 时,
时, ![]() .易知
.易知![]() 在
在![]() 递增,
递增, ![]() 递减,
递减, ![]() 递增
递增
(Ⅱ)当时,由(Ⅰ)知![]() 在
在![]() 上递增,
上递增, ![]() 上递减,
上递减, ![]() 上递增,
上递增,
且![]() ,将
,将![]() 代入
代入![]() ,
,
得![]()
∵![]() ,∴
,∴![]() .
.
下面证明 当![]() 时存在
时存在![]() ,使
,使![]() .
.
首先,由不等式![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
考虑到![]() ,
,
∴![]()
![]() .
.
再令![]() ,可解出一个根为
,可解出一个根为![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,就取
,就取![]() .
.
则有![]() .由零点存在定理及函数
.由零点存在定理及函数![]() 在
在![]() 上的单调性,可知
上的单调性,可知![]() 在
在![]() 上有唯一的一个零点.
上有唯一的一个零点.
由![]() ,及
,及![]() 的单调性,可知
的单调性,可知![]() 在
在![]() 上有唯一零点.
上有唯一零点.
下面证明在![]() 上,存在
上,存在![]() ,使
,使![]() ,就取
,就取![]() ,则
,则![]() ,
,
∴![]() ,
,
由不等式![]() ,则
,则![]() ,即
,即![]() .
.
根据零点存在定理及函数单调性知![]() 在
在![]() 上有一个零点.
上有一个零点.
综上可知, ![]() 当
当![]() 时,共有3个零点.
时,共有3个零点.
【方法点晴】本题主要考查的是利用导数研究函数的单调性、利用导数研究函数的最值、以及零点存在性定理,属于难题.利用导数研究函数![]() 的单调性的步骤:①确定函数
的单调性的步骤:①确定函数![]() 的定义域;②对
的定义域;②对![]() 求导;③令
求导;③令![]() ,解不等式得
,解不等式得![]() 的范围就是递增区间;令
的范围就是递增区间;令![]() ,解不等式得
,解不等式得![]() 的范围就是递减区间.
的范围就是递减区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
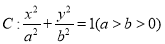 短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为
短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为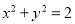 .
. (1)求椭圆
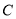 的方程;
的方程;(2)若抛物线
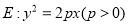 的焦点与椭圆
的焦点与椭圆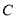 的一个焦点
的一个焦点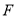 重合,直线
重合,直线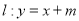 与抛物线
与抛物线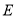 交于两点
交于两点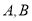 ,且
,且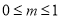 ,求
,求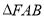 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有以下三个案例:
案例一:从同一批次同类型号的10袋牛奶中抽取3袋检测其三聚氰胺含量;
案例二:某公司有员工800人:其中高级职称的160人,中级职称的320人,初级职称200人,其余人员120人.从中抽取容量为40的样本,了解该公司职工收入情况;
案例三:从某校1000名学生中抽10人参加主题为“学雷锋,树新风”的志愿者活动.
(1)你认为这些案例应采用怎样的抽样方式较为合适?
(2)在你使用的分层抽样案例中写出每层抽样的人数;
(3)在你使用的系统抽样案例中按以下规定取得样本编号:如果在起始组中随机抽取的码为
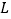 (编号从0开始),那么第
(编号从0开始),那么第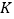 组(组号
组(组号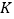 从0开始,
从0开始, )抽取的号码的百位数为组号,后两位数为
)抽取的号码的百位数为组号,后两位数为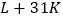 的后两位数.若
的后两位数.若 ,试求出
,试求出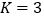 及
及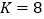 时所抽取的样本编号.
时所抽取的样本编号. -
科目: 来源: 题型:
查看答案和解析>>【题目】为对考生的月考成绩进行分析,某地区随机抽查了
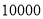 名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
名考生的成绩,根据所得数据画了如下的样本频率分布直方图.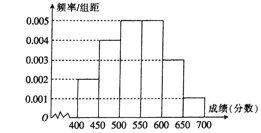
(1)求成绩在
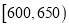 的频率;
的频率;(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析成绩与班级、学校等方面的关系,必须按成绩再从这
 人中用分层抽样方法抽取出
人中用分层抽样方法抽取出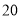 人作出进一步分析,则成绩在
人作出进一步分析,则成绩在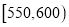 的这段应抽多少人?
的这段应抽多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 点(n,
 )在直线y=
)在直线y=  x+
x+ 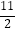 上.
上.
(1)求数列{an}的通项公式;
(2)设bn=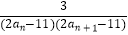 ,求数列{bn}的前n项和为Tn , 并求使不等式Tn>
,求数列{bn}的前n项和为Tn , 并求使不等式Tn> 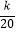 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为4的正方形
 的边上有一点
的边上有一点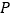 沿着折线
沿着折线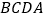 由点
由点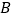 (起点)向点
(起点)向点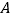 (终点)运动。设点
(终点)运动。设点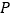 运动的路程为
运动的路程为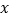 ,
,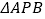 的面积为
的面积为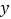 ,且
,且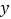 与
与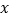 之间的函数关系式用如图所示的程序框图给出.
之间的函数关系式用如图所示的程序框图给出.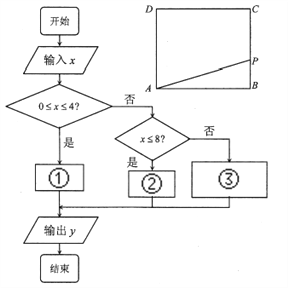
(1)写出框图中①、②、③处应填充的式子;
(2)若输出的面积
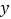 值为6,则路程
值为6,则路程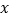 的值为多少?并指出此时点
的值为多少?并指出此时点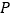 在正方形的什么位置上?
在正方形的什么位置上? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,周长为7.5cm,且sinA:sinB:sinC=4:5:6,下列结论:
①a:b:c=4:5:6 ②a:b:c=2: ③a=2cm,b=2.5cm,c=3cm ④A:B:C=4:5:6
③a=2cm,b=2.5cm,c=3cm ④A:B:C=4:5:6
其中成立的个数是( )
A.0个
B.1个
C.2个
D.3个
相关试题

