【题目】如图,在直三棱柱![]() 中,点
中,点![]() 分别为线段
分别为线段![]() 的中点.
的中点.
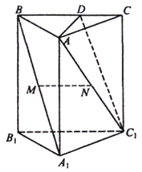
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 在边
在边![]() 上,
上,![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)详见解析(2)详见解析
【解析】
试题分析:(1)由题意,利用三角形中位线定理可证MN∥BC,即可判定MN∥平面![]() ;(2)利用线面垂直的性质可证CC1⊥AD,结合已知可证AD⊥平面
;(2)利用线面垂直的性质可证CC1⊥AD,结合已知可证AD⊥平面![]() ,从而证明AD⊥BC,结合(1)知,MN∥BC,即可证明MN⊥AD
,从而证明AD⊥BC,结合(1)知,MN∥BC,即可证明MN⊥AD
试题解析:(1)如图,连结A1C.
在直三棱柱ABC-A1B1C1中,侧面AA1C1C为平行四边形.
又因为N为线段AC1的中点,
所以A1C与AC1相交于点N,
即A1C经过点N,且N为线段A1C的中点. ……………… 2分
因为M为线段A1B的中点,
所以MN∥BC. ……………… 4分
又MN平面BB1C1C,BC平面BB1C1C,
所以MN∥平面BB1C1C. ………………… 6分
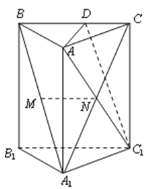
(2)在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC.
又AD平面ABC,所以CC1⊥AD. …………………… 8分
因为AD⊥DC1,DC1平面BB1C1C,CC1平面BB1C1C,CC1∩DC1=C1,
所以AD⊥平面BB1C1C. …………………… 10分
又BC平面BB1C1C,所以AD⊥BC. …………………… 12分
又由(1)知,MN∥BC,所以MN⊥AD. …………………… 14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】
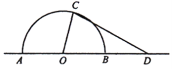
如图,某城市有一块半径为40
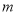 的半圆形(以
的半圆形(以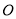 为圆心,
为圆心,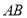 为直径)绿化区域,现计划对其进行改建,在
为直径)绿化区域,现计划对其进行改建,在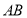 的延长线上取点
的延长线上取点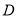 ,使
,使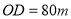 ,在半圆上选定一点
,在半圆上选定一点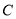 ,改建后的绿化区域由扇形区域
,改建后的绿化区域由扇形区域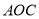 和三角形区域
和三角形区域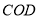 组成,其面积为
组成,其面积为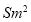 ,设
,设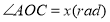
(1)写出
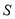 关于
关于 的函数关系式
的函数关系式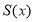 ,并指出
,并指出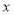 的取值范围;
的取值范围;(2)试问
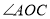 多大时,改建后的绿化区域面积
多大时,改建后的绿化区域面积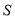 最大.
最大. -
科目: 来源: 题型:
查看答案和解析>>【题目】某渔场鱼群的最大养殖量为
 吨,为保证鱼群的生长空间,实际的养殖量
吨,为保证鱼群的生长空间,实际的养殖量 要小于
要小于 ,留出适当的空闲量,空闲量与最大养殖量的比值叫空闲率,已知鱼群的年增加量
,留出适当的空闲量,空闲量与最大养殖量的比值叫空闲率,已知鱼群的年增加量 (吨)和实际养殖量
(吨)和实际养殖量 (吨)与空闲率的乘积成正比(设比例系数
(吨)与空闲率的乘积成正比(设比例系数 ).
).(1)写出
 与
与 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;(2)求鱼群年增长量的最大值;
(3)当鱼群年增长量达到最大值时,求
 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
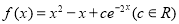 .
.(1)若
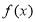 是在定义域内的增函数,求
是在定义域内的增函数,求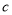 的取值范围;
的取值范围;(2)若函数
 (其中
(其中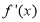 为
为 的导函数)存在三个零点,求
的导函数)存在三个零点,求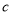 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
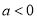 时,讨论
时,讨论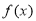 的单调性;
的单调性;(2)若对任意的
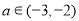 ,
, 恒有
恒有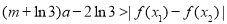 成立,求实数
成立,求实数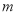 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|-1≤x≤2},B={x|m-1≤x≤2m+1},已知BA.
(1)当x∈N时,求集合A的子集的个数;
(2)求实数m的取值范围.
-
科目: 来源: 题型:
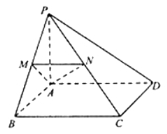
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,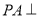 平面
平面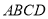 ,四边形
,四边形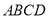 为正方形,点
为正方形,点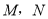 分别为线段
分别为线段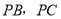 上的点,
上的点, .
.
(1)求证:平面
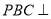 平面
平面 ;
;(2)求证:当点
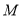 不与点
不与点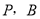 重合时,
重合时,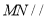 平面
平面 ;
;(3)当
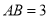 ,
,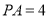 时,求点
时,求点 到直线
到直线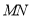 距离的最小值.
距离的最小值.
相关试题

