【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,点
为正方形,点![]() 分别为线段
分别为线段![]() 上的点,
上的点,![]() .
.
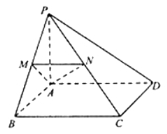
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:当点![]() 不与点
不与点![]() 重合时,
重合时,![]() 平面
平面![]() ;
;
(3)当![]() ,
,![]() 时,求点
时,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)首先运用正方形的性质与线在垂直的性质定理推出![]() 平面
平面![]() ,然后利用面面垂直的判定定理即可使问题得证;(2)结合(1)与已知条件可推出
,然后利用面面垂直的判定定理即可使问题得证;(2)结合(1)与已知条件可推出![]() ,由此根据线面平行的判定定理使问题得证;(3)根据条件可推出
,由此根据线面平行的判定定理使问题得证;(3)根据条件可推出![]() 的长就是点
的长就是点![]() 到
到![]() 的距离,从而运用点到线的距离的计算,借助转化与化归的数学思想来求解.
的距离,从而运用点到线的距离的计算,借助转化与化归的数学思想来求解.
试题解析:(1)证明:在正方形![]() 中,
中,![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)证明:由(1)知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(3)解:因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 的长就是点
的长就是点![]() 到
到![]() 的距离,
的距离,
而点![]() 在线段
在线段![]() 上,所以
上,所以![]() 到直线
到直线![]() 距离的最小值是
距离的最小值是![]() 到线段
到线段![]() 的距离,
的距离,
在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() 到直线
到直线![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
 中,点
中,点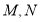 分别为线段
分别为线段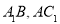 的中点.
的中点.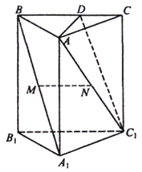
(1)求证:
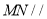 平面
平面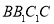 ;
;(2)若
 在边
在边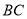 上,
上,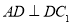 ,求证:
,求证: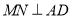 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
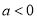 时,讨论
时,讨论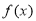 的单调性;
的单调性;(2)若对任意的
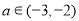 ,
, 恒有
恒有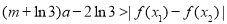 成立,求实数
成立,求实数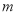 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|-1≤x≤2},B={x|m-1≤x≤2m+1},已知BA.
(1)当x∈N时,求集合A的子集的个数;
(2)求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:数列
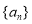 对一切正整数
对一切正整数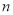 均满足
均满足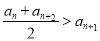 ,称数列
,称数列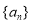 为“凸数列”,以下关于“凸数列”的说法:
为“凸数列”,以下关于“凸数列”的说法:①等差数列
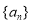 一定是凸数列;
一定是凸数列;②首项
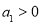 ,公比
,公比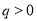 且
且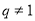 的等比数列
的等比数列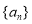 一定是凸数列;
一定是凸数列;③若数列
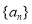 为凸数列,则数列
为凸数列,则数列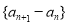 是单调递增数列;
是单调递增数列;④若数列
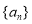 为凸数列,则下标成等差数列的项构成的子数列也为凸数列.
为凸数列,则下标成等差数列的项构成的子数列也为凸数列.其中正确说法的序号是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
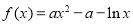 ,
,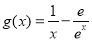 ,其中
,其中 ,
,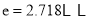 为自然对数的底数.
为自然对数的底数.(1)讨论
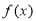 的单调性;
的单调性;(2)证明:当
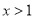 时,
时,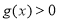 ;
;(3)确定
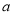 的所有可能取值,使得
的所有可能取值,使得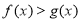 在
在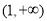 区间内恒成立.
区间内恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】设y1=
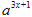 ,y2=
,y2=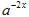 ,其中a>0,且a≠1,试确定x为何值时,有:
,其中a>0,且a≠1,试确定x为何值时,有:(1)y1=y2;(2)y1>y2.
相关试题

