【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
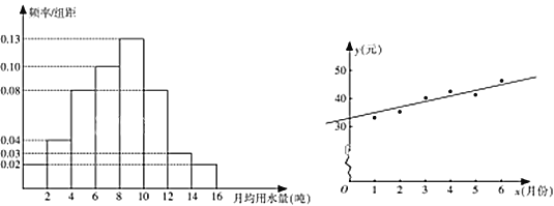
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
参考答案:
【答案】(Ⅰ)平均数为7.96,中位数为8.15;(Ⅱ)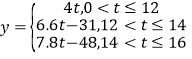 ;(Ⅲ)13吨.
;(Ⅲ)13吨.
【解析】试题分析:
本题考查频率分布直方图的应用及线性回归方程的应用。(Ⅰ)根据用频率分布直方图估计平均数、中位数的方法计算即可。(Ⅱ)结合题意可用分段函数表示出![]() 与
与![]() 的关系。(Ⅲ)先由样本中点过回归直线的结论求得1~6月份月用水费约为
的关系。(Ⅲ)先由样本中点过回归直线的结论求得1~6月份月用水费约为![]() 7月份的水费为
7月份的水费为![]() 元,再根据回归方程求得7月份的用水吨数。
元,再根据回归方程求得7月份的用水吨数。
试题解析:
(Ⅰ)由频率分布直方图可得该市居民每月的用水量的平均数为
![]()
![]() 。
。
设中位数为![]() ,
,
则![]() ,
,
解得![]() 。
。
(Ⅱ)设居民月用水量为![]() 吨,相应的水费为
吨,相应的水费为![]() 元,则由题意得
元,则由题意得
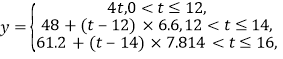
即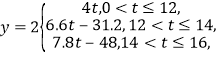
(Ⅲ)设李某2017年1~6月份月用水费![]() (元)与月份
(元)与月份![]() 的对应点为
的对应点为![]() ,它们的平均值分别为
,它们的平均值分别为![]() ,
,![]() ,
,
则![]() ,
,
又点![]() 在直线
在直线![]() 上,
上,
所以![]() ,
,
因此![]() ,
,
所以7月份的水费为![]() 元.
元.
由(2)知,当![]() 时,
时,![]() ,
,
所以李某7月份的用水吨数约为13吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形ABC的外接圆的O半径为
 ,CD垂直于外接圆所在的平面,
,CD垂直于外接圆所在的平面, 

(1)求证:平面

 平面
平面 .
.(2)试问线段
 上是否存在点
上是否存在点 ,使得直线
,使得直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ?若存在,确定点
?若存在,确定点 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知向量
 ,设
,设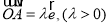 ,向量
,向量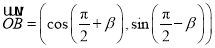 .
.(1)若
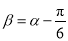 ,求向量
,求向量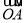 与
与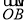 的夹角;
的夹角;(2)若
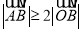 对任意实数
对任意实数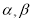 都成立,求实数
都成立,求实数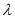 的取值范围.
的取值范围. -
科目: 来源: 题型:
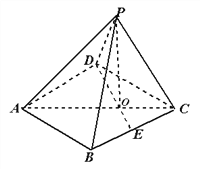
查看答案和解析>>【题目】如图,已知四棱锥
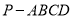 的底面的菱形,
的底面的菱形, 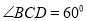 ,点E是BC边的中点,AC和DE交于点O,PO
,点E是BC边的中点,AC和DE交于点O,PO 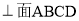 ;
;
(1)求证:
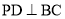 ;
; (2)
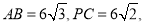 求二面角P-AD-C的大小。
求二面角P-AD-C的大小。(3)在(2)的条件下,求异面直线PB与DE所成角的余弦值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
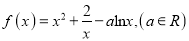 .
.(Ⅰ)若
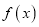 在
在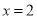 处取极值,求
处取极值,求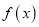 在点
在点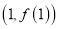 处的切线方程;
处的切线方程;(Ⅱ)当
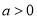 时,若
时,若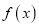 有唯一的零点
有唯一的零点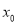 ,求证:
,求证: 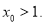
-
科目: 来源: 题型:
查看答案和解析>>【题目】【选修4-4:坐标系与参数方程】
极坐标系的极点为直角坐标系
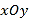 的原点,极轴为
的原点,极轴为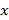 轴的正半轴,两神坐标系中的长度单位相同.已知曲线
轴的正半轴,两神坐标系中的长度单位相同.已知曲线 的极坐标方程为
的极坐标方程为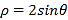 ,
, 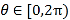 .
.(Ⅰ)求曲线
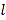 的直角坐标方程;
的直角坐标方程;(Ⅱ)在曲线
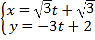 上求一点,使它到直线
上求一点,使它到直线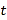 :
: 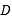 (
(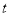 为参数)的距离最短,写出
为参数)的距离最短,写出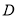 点的直角坐标.
点的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】以A表示值域为R的函数组成的集合,B表示具有如下性质的函数
 组成的集合:对于函数
组成的集合:对于函数 ,存在一个正数M,使得函数
,存在一个正数M,使得函数 的值域包含于区间
的值域包含于区间 .例如,当
.例如,当 时,
时,  . 现有如下命题:
. 现有如下命题:①设函数
 的定义域为D,则“
的定义域为D,则“ ”的充要条件是“
”的充要条件是“ ”;
”;②若函数
 ,则
,则 有最大值和最小值;
有最大值和最小值;③若函数
 的定义域相同,且
的定义域相同,且 ,则
,则 ;
;④若函数
 有最大值,则
有最大值,则 .
.其中的真命题有___________. (写出所有真命题的序号)
相关试题

