【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() .
.
(1)若![]() ,过点
,过点![]() ,
, ![]() 的直线
的直线![]() 与抛物线相交于另一点
与抛物线相交于另一点![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,与圆
两点,与圆![]() 相交于
相交于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得
,使得![]() 的长为定值?若存在,求出
的长为定值?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 时,
时, ![]() ,
, ![]() 的长为定值.
的长为定值.
【解析】试题分析:(1)根据抛物线的性质可得![]() 到焦点
到焦点![]() 的距离为
的距离为![]() 可得出
可得出![]() ,求出
,求出![]() 的方程,联立抛物线
的方程,联立抛物线![]() ,故而可得
,故而可得![]() ,
, ![]() ,即可得最后结果;(2)设出直线
,即可得最后结果;(2)设出直线![]() 的方程为
的方程为![]() ,设
,设![]()
![]() ,与抛物线方程联立,运用韦达定理得
,与抛物线方程联立,运用韦达定理得![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,将
,将![]() ,
, ![]() 代入可得
代入可得![]() 的值,利用直线截圆所得弦长公式得
的值,利用直线截圆所得弦长公式得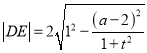 ,故当
,故当![]() 时满足题意.
时满足题意.
试题解析:(1)∵点![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
故抛物线![]() 的方程为:
的方程为: ![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 的方程为
的方程为![]() ,联立
,联立![]() 可得,
可得, ![]() ,
,
又∵![]() ,
, ![]() ,∴
,∴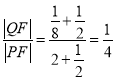 .
.
(2)设直线![]() 的方程为
的方程为![]() ,代入抛物线方程可得
,代入抛物线方程可得![]() ,
,
设![]()
![]() ,则
,则![]() ,
, ![]() ,①
,①
由![]() 得:
得: ![]() ,
,
整理得![]() ,②
,②
将①代入②解得![]() ,∴直线
,∴直线![]() ,
,
∵圆心到直线l的距离![]() ,∴
,∴ ,
,
显然当![]() 时,
时, ![]() ,
, ![]() 的长为定值.
的长为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设向量
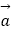 =(
=( 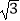 sinx,sinx),
sinx,sinx), 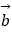 =(cosx,sinx),x∈[0,
=(cosx,sinx),x∈[0,  ].
].
(1)若|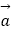 |=|
|=| 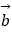 |,求x的值;
|,求x的值;
(2)设函数f(x)=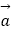
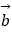 ,求f(x)的最大值及单调递增区间.
,求f(x)的最大值及单调递增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:

(Ⅰ)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(Ⅱ)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x﹣2)2+(y﹣3)2=1交于点M、N两点.
(1)求k的取值范围;
(2)若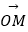
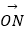 =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|. -
科目: 来源: 题型:
查看答案和解析>>【题目】为研究患肺癌与是否吸烟有关,做了一次相关调查,其中部分数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的
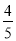 ;不吸烟的人数中,患肺癌与不患肺癌的比为
;不吸烟的人数中,患肺癌与不患肺癌的比为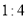 .
.(1)若吸烟不患肺癌的有
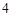 人,现从患肺癌的人中用分层抽样的方法抽取
人,现从患肺癌的人中用分层抽样的方法抽取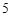 人,再从这
人,再从这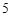 人中随机抽取
人中随机抽取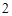 人进行调查,求这两人都是吸烟患肺癌的概率;
人进行调查,求这两人都是吸烟患肺癌的概率;(2)若研究得到在犯错误概率不超过
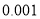 的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?
的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?附:
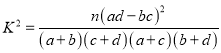 ,其中
,其中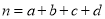 .
.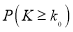
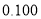
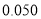
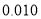
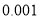
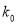
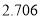
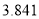
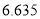
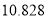
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
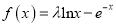 (
(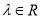 ).
).(1)若函数
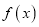 是单调函数,求
是单调函数,求 的取值范围;
的取值范围;(2)求证:当
 时,都有
时,都有 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某网站针对2014年中国好声音歌手A,B,C三人进行网上投票,结果如下:
观众年龄
支持A
支持B
支持C
20岁以下
200
400
800
20岁以上(含20岁)
100
100
400
(1)在所有参与该活动的人中,用分层抽样的方法抽取n人,其中有6人支持A,求n的值.
(2)在支持C的人中,用分层抽样的方法抽取6人作为一个总体,从这6人中任意选取2人,求恰有1人在20岁以下的概率.
相关试题

