【题目】设向量 ![]() =(
=( ![]() sinx,sinx),
sinx,sinx), ![]() =(cosx,sinx),x∈[0,
=(cosx,sinx),x∈[0, ![]() ].
].
(1)若| ![]() |=|
|=| ![]() |,求x的值;
|,求x的值;
(2)设函数f(x)= ![]()
![]() ,求f(x)的最大值及单调递增区间.
,求f(x)的最大值及单调递增区间.
参考答案:
【答案】
(1)解:依题意知3sin2x+sin2x=cos2x+sin2x=1
∴sin2x= ![]() ,
,
∵x∈[0, ![]() ].
].
∴sinx= ![]() ,
,
x= ![]() .
.
(2)解:f(x)= ![]()
![]() =
= ![]() sinxcosx+sin2x=
sinxcosx+sin2x= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+
cos2x+ ![]() =sin(2x﹣
=sin(2x﹣ ![]() )+
)+ ![]() ,
,
f(x)max=1+ ![]() =
= ![]() ,
,
由2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,得kπ﹣
,k∈Z,得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
∴函数的单调增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
【解析】(1)先根据题意分别表示出两向量的模,取得sinx的值,进而求得x.(2)表示出函数f(x)的表达式,进而利用二倍角公式和两角和公式化简,进而根据三角函数的图象和性质求得函数的最大值和单调增区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校有体育特长生25人,美术特长生35人,音乐特长生40人.用分层抽样的方法从中抽取40人,则抽取的体育特长生、美术特长生、音乐特长生的人数分别为( )
A.8,14,18
B.9,13,18
C.10,14,16
D.9,14,17 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校有高级教师20人,中级教师30人,其他教师若干人,为了了解该校教师的工资收入情况,拟按分层抽样的方法从该校所有的教师中抽取20人进行调查.已知从其他教师中共抽取了10人,则该校共有教师人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆O上的点.
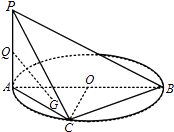
(1)求证:BC⊥平面PAC;
(2)若Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:

(Ⅰ)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(Ⅱ)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x﹣2)2+(y﹣3)2=1交于点M、N两点.
(1)求k的取值范围;
(2)若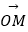
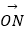 =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 在第一象限内的点
在第一象限内的点 到焦点
到焦点 的距离为
的距离为 .
.(1)若
 ,过点
,过点 ,
,  的直线
的直线 与抛物线相交于另一点
与抛物线相交于另一点 ,求
,求 的值;
的值;(2)若直线
 与抛物线
与抛物线 相交于
相交于 两点,与圆
两点,与圆 相交于
相交于 两点,
两点,  为坐标原点,
为坐标原点,  ,试问:是否存在实数
,试问:是否存在实数 ,使得
,使得 的长为定值?若存在,求出
的长为定值?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

