【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),圆
为参数),圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直线
为参数).若直线![]() 分别与圆
分别与圆![]() 和圆
和圆![]() 交于不同于原点的点
交于不同于原点的点![]() 和
和![]() .
.
(1)以直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,求圆
轴的正半轴为极轴,建立极坐标系,求圆![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)求![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)首先写出直角坐标方程,然后转化为极坐标方程可得圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(2)直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),结合极坐标方程的几何意义计算可得
),结合极坐标方程的几何意义计算可得![]() 的面积为
的面积为![]() .
.
(1)由题意可知,圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,即
,即![]() ,
,
∴极坐标方程为![]() ,
,
由题意可知,圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,即
,即![]() ,
,
∴极坐标方程为![]() .
.
(2)直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),
),
∵直线![]() 与圆
与圆![]() ,
,![]() 交于不同于原点的点
交于不同于原点的点![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴![]() ,
,
∴![]() 的面积为
的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
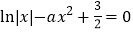 有4个不同的实数根,则实数
有4个不同的实数根,则实数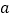 的取值范围是( )
的取值范围是( )A.
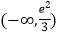 B.
B. 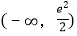 C.
C. 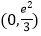 D.
D. 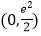
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是奇函数.
是奇函数.(1)求a的值和函数f(x)的定义域;
(2)解不等式f(-m2+2m-1)+f(m2+3)<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sinxcosx﹣
 x.
x.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)当x∈[0, ]时,求f(x)的最大值和最小值.
]时,求f(x)的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学准备在开学时举行一次大学一年级学生座谈会,拟邀请20名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
学院
机械工程学院
海洋学院
医学院
经济学院
人数
4
6
4
6
(Ⅰ)从这20名学生中随机选出3名学生发言,求这3名学生中任意两个均不属于同一学院的概率;
(Ⅱ)从这20名学生中随机选出3名学生发言,设来自医学院的学生数为ξ,求随机变量ξ的概率分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
(Ⅰ)若BM=2MP,求证:PD∥平面MAC;
(Ⅱ)若平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,求证:PA⊥平面ABCD;
(Ⅲ)在(Ⅱ)的条件下,若二面角B﹣AC﹣M的余弦值为 ,求
,求 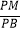 的值.
的值.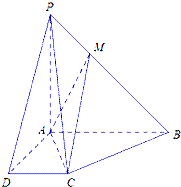
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N* , 总有b1b2b3…bn﹣1bn=an+2成立.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记cn=(﹣1)n ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
相关试题

