【题目】已知正项等比数列![]() 的前
的前![]() 项和为
项和为![]() ,首项
,首项![]() ,且
,且![]() ,正项数列
,正项数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)记![]()
![]() ,是否存在正整数
,是否存在正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,
,![]() 恒成立?若存在,求正整数
恒成立?若存在,求正整数![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;
;![]() (2)见解析
(2)见解析
【解析】
(1)先设等比数列![]() 的公比为
的公比为![]() ,根据题中条件,求出公比,即可得出
,根据题中条件,求出公比,即可得出![]() 的通项公式;再由累乘法求出
的通项公式;再由累乘法求出![]() ,根据题中条件求出
,根据题中条件求出![]() ,
,![]() 代入验证,即可得出
代入验证,即可得出![]() 的通项公式;
的通项公式;
(2)先由(1)化简![]() ,根据
,根据![]() ,求出
,求出![]() 的最大值,进而可得出结果.
的最大值,进而可得出结果.
解:(1)设等比数列![]() 的公比为
的公比为![]() ,
,
由![]() ,得
,得![]() ,
,
又![]() ,则
,则![]() ,
,
所以![]() .
.
![]() ,由
,由![]() ,得
,得
![]() ,
,![]() ,…,
,…,![]() ,
,
以上各式相乘得:![]() ,所以
,所以![]() .
.
在![]() 中,分别令
中,分别令![]() ,
,![]() ,得
,得![]() ,
,![]() 满足
满足![]() .
.
因此![]() .
.
(2)由(1)知![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
令![]() ,得
,得![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴当![]() 时,
时,![]() ,即
,即![]() .
.
∵当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() .
.
此时![]() ,即
,即![]() ,
,
∴![]() 的最大值为
的最大值为![]() .
.
若存在正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,
,![]() 恒成立,则
恒成立,则![]() ,
,
∴正整数![]() 的最小值为4.
的最小值为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,圆C的参数方程为
 (θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(1)求圆C的极坐标方程;
(2)若直线l的极坐标方程是 ,射线
,射线 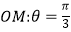 与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
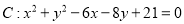 .
.(1)若直线
 过定点
过定点 ,且与圆
,且与圆 相切,求
相切,求 的方程;
的方程;(2)若圆
 的半径为
的半径为 ,圆心在直线
,圆心在直线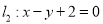 上,且与圆
上,且与圆 外切,求圆
外切,求圆 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记1分,海选不合格记0分.假设甲、乙、丙海选合格的概率分别为
 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;
(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量
 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣a|+2|x+b|(a>0,b>0)的最小值为1.
(1)求a+b的值;
(2)若 恒成立,求实数m的最大值.
恒成立,求实数m的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平行六面体
 中,
中, .
.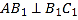
求证:(1)
 ;
;(2)
 .
.
相关试题

