【题目】已知函数f(x)=|x﹣a|+2|x+b|(a>0,b>0)的最小值为1.
(1)求a+b的值;
(2)若 ![]() 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
参考答案:
【答案】
(1)解: 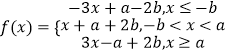
f(x)在区间(﹣∞,﹣b]上递减,在区间[﹣b,+∞)上递增,
所以f(x)min=a+b.
所以a+b=1.
(2)解:因为a>0,b>0,且a+b=1,
所以 ![]() ,
,
又因为 ![]() ,当且仅当
,当且仅当 ![]() 时,等号成立,
时,等号成立,
所以 ![]() 时,
时, ![]() 有最小值
有最小值 ![]() .
.
所以 ![]() ,所以实数m的最大值为
,所以实数m的最大值为 ![]()
【解析】(1)写出分段函数,得出f(x)min=a+b,即可求a+b的值;(2)因为a>0,b>0,且a+b=1,利用“1”的代换,求最值,根据 ![]() 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
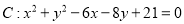 .
.(1)若直线
 过定点
过定点 ,且与圆
,且与圆 相切,求
相切,求 的方程;
的方程;(2)若圆
 的半径为
的半径为 ,圆心在直线
,圆心在直线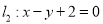 上,且与圆
上,且与圆 外切,求圆
外切,求圆 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记1分,海选不合格记0分.假设甲、乙、丙海选合格的概率分别为
 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;
(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量
 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项等比数列
 的前
的前 项和为
项和为 ,首项
,首项 ,且
,且 ,正项数列
,正项数列 满足
满足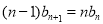 ,
, .
.(1)求数列
 ,
, 的通项公式;
的通项公式;(2)记

 ,是否存在正整数
,是否存在正整数 ,使得对任意正整数
,使得对任意正整数 ,
, 恒成立?若存在,求正整数
恒成立?若存在,求正整数 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平行六面体
 中,
中, .
.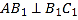
求证:(1)
 ;
;(2)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.?x,y∈R,若x+y≠0,则x≠1且y≠﹣1
B.a∈R,“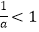 ”是“a>1”的必要不充分条件
”是“a>1”的必要不充分条件
C.命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0”
D.设随机变量X~N(1,52),若P(X<0)=P(X>a﹣2),则实数a的值为2
相关试题

