【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 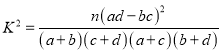 ,其中
,其中![]() )
)
参考答案:
【答案】(1)详见解析;(2)有![]() ﹪的把握认为喜爱打篮球与性别有关.
﹪的把握认为喜爱打篮球与性别有关.
【解析】试题分析:(1)根据在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() ,可得喜爱打篮球的学生,即可得到列联表;(2)利用公式求得
,可得喜爱打篮球的学生,即可得到列联表;(2)利用公式求得![]() ,与临界值比较,即可得到结论
,与临界值比较,即可得到结论
试题解析:(1) 已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为![]()
列联表如下:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(2)∵![]()
∴有99.5%的把握认为喜爱打篮球与性别有关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
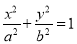 (
(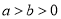 )的离心率为
)的离心率为 ,短轴的一个端点为
,短轴的一个端点为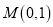 .过椭圆左顶点
.过椭圆左顶点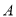 的直线
的直线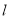 与椭圆的另一交点为
与椭圆的另一交点为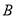 .
.(1)求椭圆的方程;
(2)若
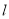 与直线
与直线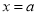 交于点
交于点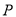 ,求
,求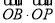 的值;
的值;(3)若
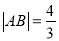 ,求直线
,求直线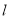 的倾斜角.
的倾斜角. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的参数方程为
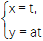 (t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.(1)求点Q的轨迹C2的直角坐标方程;
(2)直线l与直线C2交于A,B两点,若|AB|≥2
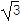 ,求实数a的取值范围.
,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点
 的直线与圆
的直线与圆 相交于
相交于 两点,过点
两点,过点 且与
且与 垂直的直线与圆
垂直的直线与圆 的另一交点为
的另一交点为 .
.
(1)当点
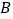 坐标为
坐标为 时,求直线
时,求直线 的方程;
的方程;(2)求四边形
 面积
面积 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,平面
 平面
平面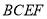 ,且四边形
,且四边形 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形,  ,
, 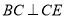 ,
, 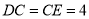 ,
, 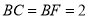 .
.
(1)求证:
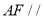 平面
平面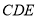 ;
;(2)求直线
 与平面
与平面 所成角的余弦值;
所成角的余弦值; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
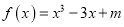 ,若在区间
,若在区间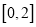 上任取三个数
上任取三个数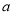 、
、 、
、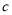 ,均存在以
,均存在以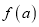 、
、 、
、 为边长的三角形,则实数
为边长的三角形,则实数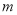 的取值范围为__________.
的取值范围为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱柱
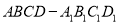 中,底面
中,底面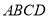 是矩形,且
是矩形,且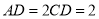 ,
, 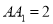 ,
, 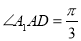 ,若
,若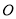 为
为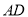 的中点,且
的中点,且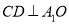 .
.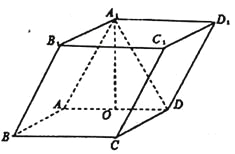
(Ⅰ)求证:
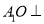 平面
平面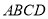 ;
;(Ⅱ)线段
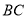 上是否存在一点
上是否存在一点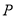 ,使得二面角
,使得二面角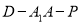 的大小为
的大小为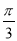 ?若存在,求出
?若存在,求出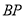 的长;若不存在,说明理由.
的长;若不存在,说明理由.
相关试题

