【题目】已知直线![]() 经过点A
经过点A![]() ,求:
,求:
(1)直线![]() 在两坐标轴上的截距相等的直线方程;
在两坐标轴上的截距相等的直线方程;
(2)直线![]() 与两坐标轴的正半轴围成三角形面积最小时的直线方程.
与两坐标轴的正半轴围成三角形面积最小时的直线方程.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)当直线过原点时,方程为 y=3x,当直线不过原点时,设直线的方程为:x+y=k,把点(1,3)代入直线的方程可得k值,即得所求的直线方程;(2)设直线方程为:![]() ,根据三角形的面积公式和基本不等式即可求出最值,继而得到直线方程
,根据三角形的面积公式和基本不等式即可求出最值,继而得到直线方程
试题解析:(1)若直线![]() 的截距为
的截距为![]() ,则直线方程为
,则直线方程为![]() ;
;
若直线![]() 的截距不为零,则可设直线方程为:
的截距不为零,则可设直线方程为:![]() ,由题设有
,由题设有
![]() , 所以直线方程为:
, 所以直线方程为:![]() ,
,
综上,所求直线的方程为![]() 。
。
(2)设直线方程为:![]() ,
, ![]() ,而面积
,而面积![]() ,
,
又由![]() 得
得 ![]() ,
,
等号当且仅当![]() 成立, 即当
成立, 即当![]() 时,面积最小为12
时,面积最小为12
所求直线方程为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的三视图如下图所示,其中主视图与左视图是腰长为6的等腰直角三角形,俯视图是正方形.

(Ⅰ)请画出该几何体的直观图,并求出它的体积;
(Ⅱ)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1? 如何组拼?试证明你的结论;
(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
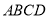 与
与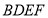 均为菱形,
均为菱形,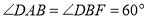 ,且
,且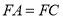 .
.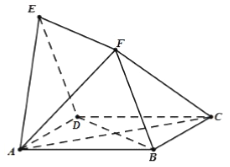
(1)求证:
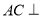 平面
平面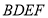 ;
;(2)求证:
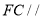 平面
平面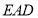 ;
;(3)求二面角
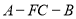 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校100名学生其中考试语文成绩的频率分布直方图所示,其中成绩分组区间是:
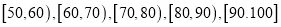 .
.(1)求图中
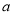 的值;
的值;(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文某些分数段的人数
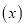 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数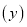 之比如下表所示,
之比如下表所示,求数学成绩在
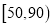 之外的人数.
之外的人数.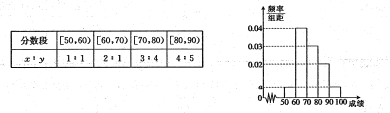
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
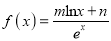 (
(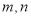 为常数,
为常数, 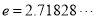 是自然对数的底数),曲线
是自然对数的底数),曲线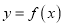 在点
在点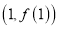 处的切线方程是
处的切线方程是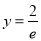 .
.(1)求
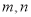 的值;(2)求
的值;(2)求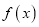 的单调区间;
的单调区间;(3)设
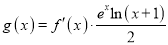 (其中
(其中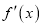 为
为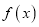 的导函数)。证明:对任意
的导函数)。证明:对任意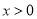 ,
, 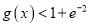
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)求函数
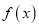 的单调区间;
的单调区间;(2)当
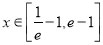 时,是否存在整数
时,是否存在整数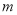 ,使不等式
,使不等式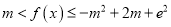 恒成立?若存在,求整数
恒成立?若存在,求整数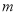 的值;若不存在,则说明理由;
的值;若不存在,则说明理由;(3)关于
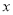 的方程
的方程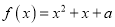 在
在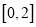 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数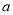 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列
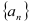 的前
的前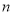 项和为
项和为 ,
,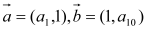 ,若
,若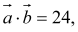 且
且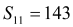 ,数列
,数列 的前
的前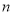 项和为
项和为 ,且满足
,且满足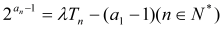 .
.(Ⅰ)求数列
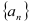 的通项公式及数列
的通项公式及数列 的前
的前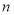 项和
项和 ;
;(Ⅱ)是否存在非零实数
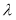 ,使得数列
,使得数列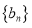 为等比数列?并说明理由.
为等比数列?并说明理由.
相关试题

