【题目】设点![]() 到坐标原点的距离和它到直线
到坐标原点的距离和它到直线![]() 的距离之比是一个常数
的距离之比是一个常数![]() .
.
(1)求点![]() 的轨迹;
的轨迹;
(2)若![]() 时得到的曲线是
时得到的曲线是![]() ,将曲线
,将曲线![]() 向左平移一个单位长度后得到曲线
向左平移一个单位长度后得到曲线![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,过
,过![]() 的直线
的直线![]() 分别交曲线
分别交曲线![]() 于点
于点![]() ,设
,设![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析: (1)设![]() ,直接法求出点
,直接法求出点![]() 的轨迹方程,由轨迹方程判断出轨迹; (2)由已知条件求出曲线E的方程,利用向量坐标运算求出
的轨迹方程,由轨迹方程判断出轨迹; (2)由已知条件求出曲线E的方程,利用向量坐标运算求出![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,联立直线
,联立直线![]() 的方程和曲线E的方程,利用韦达定理求出
的方程和曲线E的方程,利用韦达定理求出![]() ,再求出
,再求出![]() 的范围.
的范围.
试题解析:(Ⅰ)过点![]() 作
作![]() ,
, ![]() 为垂足,
为垂足,
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() ,
,
故点![]() 的轨迹方程为
的轨迹方程为![]() .
.
可化为![]() ,显然点
,显然点![]() 的轨迹为焦点在
的轨迹为焦点在![]() 轴上的椭圆.
轴上的椭圆.
(Ⅱ)![]() 时,得到的曲线
时,得到的曲线![]() 的方程是
的方程是![]() ,
,
故曲线![]() 的方程是
的方程是![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() .
.
当![]() 与
与![]() 轴不垂直时,直线
轴不垂直时,直线![]() 的方程为
的方程为![]() ,即
,即![]() ,代入曲线
,代入曲线![]() 的方程并注意到
的方程并注意到![]() ,
,
整理可得![]() ,
,
则![]() ,即
,即![]() ,于是
,于是![]() .
.
当![]() 与
与![]() 轴垂直时,A点的横坐标为
轴垂直时,A点的横坐标为![]() ,
, ![]() ,显然
,显然![]() 也成立.
也成立.
同理可得![]() .
.
设直线![]() 的方程为
的方程为![]() ,联立
,联立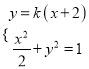 ,
,
消去y整理得![]() ,
,
由![]() 及
及![]() ,解得
,解得![]() .
.
又![]() ,
,
则![]() .
.
故求![]() 的取值范围是
的取值范围是![]() .
.
点睛:本题考查了轨迹方程的求法以及直线与椭圆相交时相关问题,属于中档题.在(1)中,求轨迹与求轨迹方程不一样,把轨迹方程求出来后,再判断是什么类型的曲线;在(2)中,注意向量坐标运算求出![]() 的表达式,再联立直线
的表达式,再联立直线![]() 的方程和椭圆方程求出
的方程和椭圆方程求出![]() ,进而求出
,进而求出![]() 的范围.
的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
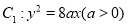 ,直线
,直线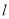 倾斜角是
倾斜角是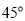 且过抛物线
且过抛物线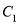 的焦点,直线
的焦点,直线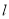 被抛物线
被抛物线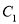 截得的线段长是16,双曲线
截得的线段长是16,双曲线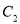 :
: 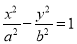 的一个焦点在抛物线
的一个焦点在抛物线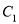 的准线上,则直线
的准线上,则直线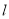 与
与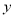 轴的交点
轴的交点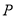 到双曲线
到双曲线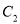 的一条渐近线的距离是( )
的一条渐近线的距离是( )A. 2 B.
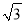 C.
C. 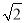 D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】将圆
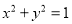 上每一点的纵坐标不变,横坐标变为原来的
上每一点的纵坐标不变,横坐标变为原来的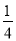 ,得曲线C.
,得曲线C.(Ⅰ)写出C的参数方程;
(Ⅱ)设直线l:
 与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设圆的方程为x2+y2=4,过点M(0,1)的直线l交圆于点A、B,O是坐标原点,点P为AB的中点,当l绕点M旋转时,求动点P的轨迹方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格纸上小正方形的边长为
 ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥
 的底面为矩形,D为
的底面为矩形,D为 的中点,AC⊥平面BCC1B1.
的中点,AC⊥平面BCC1B1.
(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=
 ,
,(1)求BD的长;
(2)求B1D与平面ABB1所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
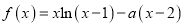 .
.(1)若
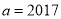 ,求曲线
,求曲线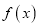 在
在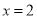 处的切线方程;
处的切线方程;(2)若当
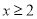 时,
时, 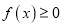 ,求
,求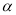 的取值范围.
的取值范围.
相关试题

