搜索
【题目】如图，网格纸上小正方形的边长为
，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（ ）
A. 
B. 
C. 
D. 
参考答案：
【答案】B
【解析】由题意，该几何体是一个组合体，下半部分是一个底面半径为3，高为4的圆柱，其体积
，上半部分是一个底面半径为3，高为6的圆柱的一半，其体积
，故该组合体的体积
．故选B．
点睛:在由三视图还原为空间几何体的实际形状时，要从三个视图综合考虑，根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线在三视图中为虚线．在还原空间几何体实际形状时，一般是以正视图和俯视图为主，结合侧视图进行综合考虑．求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将圆
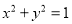上每一点的纵坐标不变，横坐标变为原来的
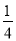，得曲线C.（Ⅰ）写出C的参数方程；
（Ⅱ）设直线l：
与C的交点为P1，P2，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求过线段P1 P2的中点且与l垂直的直线的极坐标方程. -
科目： 来源： 题型：
查看答案和解析>>【题目】设圆的方程为x2＋y2＝4，过点M(0,1)的直线l交圆于点A、B，O是坐标原点，点P为AB的中点，当l绕点M旋转时，求动点P的轨迹方程.
-
科目： 来源： 题型：
查看答案和解析>>【题目】设点
到坐标原点的距离和它到直线
的距离之比是一个常数
．（1）求点
的轨迹；（2）若
时得到的曲线是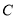
，将曲线
向左平移一个单位长度后得到曲线
，过点
的直线
与曲线
交于不同的两点
，过
的直线
分别交曲线
于点
，设
， 
， 
，求
的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四棱锥
的底面为矩形，D为
的中点，AC⊥平面BCC1B1．
（Ⅰ）证明：AB//平面CDB1;
（Ⅱ）若AC=BC=1，BB1=
,（1）求BD的长；
（2）求B1D与平面ABB1所成角的正弦值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设函数
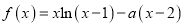．（1）若
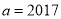，求曲线
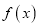在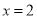
处的切线方程；（2）若当
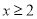时， 
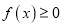，求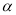
的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由20名高二级学生和15名高一级学生组成，现采用分层抽样的方法抽取7人，组成一个体验小组去市场体验“共享单车”的使用.问：
（Ⅰ）应从该兴趣小组中抽取高一级和高二级的学生各多少人；
（Ⅱ）已知该地区有
, 
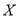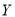两种型号的“共享单车”，在市场体验中，该体验小组的高二级学生都租
型车，高一级学生都租
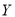型车.（1）如果从组内随机抽取3人，求抽取的3人中至少有2人在市场体验过程中租
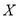型车的概率;（2）已知该地区
型车每小时的租金为1元， 
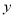型车每小时的租金为1.2元，设
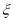为从体验小组内随机抽取3人得到的每小时租金之和，求
的数学期望.
相关试题
