【题目】已知与曲线![]() 相切的直线
相切的直线![]() ,与
,与![]() 轴,
轴, ![]() 轴交于
轴交于![]() 两点,
两点, ![]() 为原点,
为原点, ![]() ,
, ![]() ,(
,( ![]() ).
).
(1)求证:: ![]() 与
与![]() 相切的条件是:
相切的条件是: ![]() .
.
(2)求线段![]() 中点的轨迹方程;
中点的轨迹方程;
(3)求三角形![]() 面积的最小值.
面积的最小值.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)写出直线的截距式方程,化为一般式,化圆的一般式方程为标准式,求出圆心坐标和半径,由圆心到直线的距离等于半径得到曲线C与直线l相切的充要条件;
(2)设出线段AB的中点坐标,由中点坐标公式得到a,b与AB中点坐标的关系,代入(1)中的条件得线段AB中点的轨迹方程.(3)因为a与b都大于2,且三角形AOB为直线三角形,要求面积的最小值即要求ab的最小值,根据(1)中直线l与圆相切的条件(a-2)(b-2)=2解出ab,然后利用基本不等式即可求出ab最小时当且经当a与b相等,求出此时的a与b即可求出面积的最小值.
试题解析:
(1)圆的圆心为![]() ,半径为1.可以看作是
,半径为1.可以看作是![]() 的内切圆。
的内切圆。
内切圆的半径![]() ,
,
即![]() ,
,
![]() 即
即![]() ,
,
![]() .
.
(2)线段AB中点![]() 为
为![]()
∴![]() (
(![]() )
)
(3) ![]() ,
,
![]()
![]() ,
,
解得![]() ,
, ![]() ,
,
![]() ,
,
![]() 最小面积
最小面积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
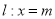 (
(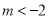 )与
)与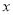 轴交于
轴交于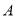 点,动圆
点,动圆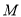 与直线
与直线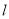 相切,并且与圆
相切,并且与圆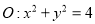 相外切,
相外切,(1)求动圆的圆心
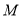 的轨迹
的轨迹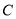 的方程;
的方程;(2)若过原点且倾斜角为
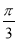 的直线与曲线
的直线与曲线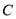 交于
交于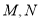 两点,问是否存在以
两点,问是否存在以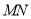 为直径的圆经过点
为直径的圆经过点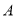 ?若存在,求出
?若存在,求出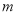 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式为12x2﹣ax>a2 .
(1)当a=2时,求不等式的解集;
(2)当a∈R时,求不等式的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两条直线l1(3+m)x+4y=5﹣3m,l2 2x+(5+m)y=8.当m分别为何值时,l1与l2:
(1)相交?
(2)平行?
(3)垂直? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市2017年3月1日至16日的空气质量指数趋势图,空气质量指数
 小于
小于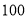 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于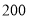 表示空气重度污染.
表示空气重度污染. 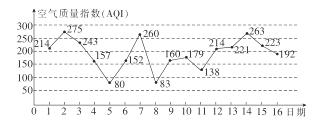
(1)若该人随机选择3月1日至3月14日中的某一天到达该市,到达后停留
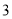 天(到达当日算
天(到达当日算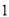 天),求此人停留期间空气重度污染的天数为
天),求此人停留期间空气重度污染的天数为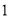 天的概率;
天的概率;(2)若该人随机选择3月7日至3月12日中的
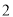 天到达该市,求这
天到达该市,求这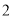 天中空气质量恰有
天中空气质量恰有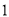 天是重度污染的概率.
天是重度污染的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第
 年与年销量
年与年销量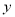 (单位:万件)之间的关系如下表:
(单位:万件)之间的关系如下表:
(1)在图中画出表中数据的散点图;
(2)根据散点图选择合适的回归模型拟合
 与
与 的关系(不必说明理由);
的关系(不必说明理由);(3)建立
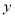 关于
关于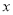 的回归方程,预测第5年的销售量.
的回归方程,预测第5年的销售量.附注:参考公式:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
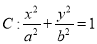 (
(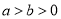 ),若椭圆
),若椭圆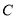 上的一动点到右焦点的最短距离为
上的一动点到右焦点的最短距离为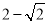 ,且右焦点到直线
,且右焦点到直线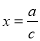 的距离等于短半轴的长,已知
的距离等于短半轴的长,已知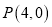 ,过
,过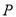 的直线与椭圆交于
的直线与椭圆交于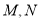 两点.
两点.(1)求椭圆
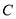 的方程;
的方程;(2)求
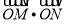 的取值范围.
的取值范围.
相关试题

