【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足![]() .
.
(1)求角B的大小;
(2)若点M为BC中点,且AM=AC=2,求a的值.
参考答案:
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】试题分析:(1)先利用正弦定理将条件中边角关系转化为角的关系: ![]() 再利用两角和正弦公式、诱导公式、三角形内角关系,配角公式化为
再利用两角和正弦公式、诱导公式、三角形内角关系,配角公式化为![]() ,最后根据特殊角的三角函数值及三角形内角范围确定角B的大小;(2)利用AM=AC构造直角三角形:取CM中点D, 则△ADB为直角三角形,解出
,最后根据特殊角的三角函数值及三角形内角范围确定角B的大小;(2)利用AM=AC构造直角三角形:取CM中点D, 则△ADB为直角三角形,解出![]() .最后根据余弦定理
.最后根据余弦定理![]() ,得
,得![]() .
.
试题解析:(1) 
即![]() .
.
∴![]() ,∴
,∴![]() ,所以
,所以![]() ,得
,得![]() .
.
(2)取CM中点D,连AD,则AD⊥CM,设![]() ,则
,则![]() .
.
由(1)知![]() ,在直角△ADB中,
,在直角△ADB中, 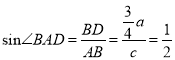 ,∴
,∴![]() .
.
在△ABC中,由余弦定理: ![]() ,
,
即![]() ,得
,得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥S﹣ABC中,SA⊥AB,SA⊥AC,AC⊥BC且AC=2,BC=
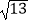 , SB=
, SB=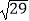 .
.
(1)证明:SC⊥BC;
(2)求三棱锥的体积VS﹣ABC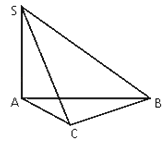
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.
(Ⅰ)求证:AC⊥DE;
(Ⅱ)求四棱锥P﹣ABCD的体积.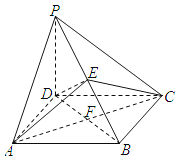
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P﹣ABC中,AB⊥平面PAC,∠APC=90°,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.
(Ⅰ)证明:平面PCE⊥平面PAB;
(Ⅱ)证明:MN∥平面PAC.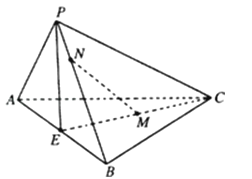
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知圆
 的圆心在直线
的圆心在直线 上,且过点
上,且过点 ,与直线
,与直线 相切.
相切.(
 )求圆
)求圆 的方程.
的方程.(
 )设直线
)设直线 与圆
与圆 相交于
相交于 ,
, 两点.求实数
两点.求实数 的取值范围.
的取值范围.(
 )在(
)在( )的条件下,是否存在实数
)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱锥
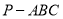 的三个侧面均为边长是
的三个侧面均为边长是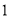 的等边三角形,
的等边三角形, 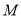 ,
, 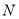 分别为
分别为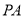 ,
, 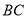 的中点.
的中点.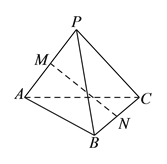
(I)求
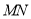 的长.
的长.(II)求证:
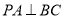 .
.(III)求三棱锥
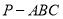 的表面积.
的表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P﹣ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
(1)判定AE与PD是否垂直,并说明理由.
(2)设AB=2,若H为PD上的动点,若△AHE面积的最小值为 , 求四棱锥P﹣ABCD的体积.
, 求四棱锥P﹣ABCD的体积.
相关试题

