
【题目】已知函数![]()
(1)若函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求导得到![]() ,讨论
,讨论![]() 和
和![]() 两种情况,计算函数的单调性,得到
两种情况,计算函数的单调性,得到![]() ,再讨论
,再讨论![]() ,
,![]() ,
,![]() 三种情况,计算得到答案.
三种情况,计算得到答案.
(2)计算得到![]() ,讨论
,讨论![]() ,
,![]() 两种情况,分别计算单调性得到函数最值,得到答案.
两种情况,分别计算单调性得到函数最值,得到答案.
(1)![]() ,
,
①当![]() 时
时![]() 恒成立,所以
恒成立,所以![]() 单调递增,因为
单调递增,因为![]() ,所以
,所以![]() 有唯一零点,即
有唯一零点,即![]() 符合题意;
符合题意;
②当![]() 时,令
时,令![]() ,
,
函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,函数
上单调递增,函数![]() 。
。
(i)当即![]() ,
,![]() 所以
所以![]() 符合题意,
符合题意,
(ii)当即![]() 时
时![]() ,
,
因为![]() ,
,
故存在![]() ,
,![]() 所以
所以![]() 不符题意
不符题意
(iii)当![]() 时
时![]() ,
,
因为![]() ,
,
设![]() ,
,
所以![]() ,
,![]() 单调递增,即
单调递增,即![]() ,
,
故存在![]() ,使得
,使得![]() ,不符题意;
,不符题意;
综上,![]() 的取值范围为
的取值范围为![]() 。
。
(2)![]() 。
。
①当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 单调递增,所以
单调递增,所以![]() ,
,
即![]() 符合题意;
符合题意;
②当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 单调递增,
单调递增,
又因为![]() ,
,
所以存在![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时,![]() 。
。
即![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,不符题意。
,不符题意。
综上,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )

A.2017年第一季度GDP增速由高到低排位第5的是浙江省
B.2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
C.去年同期河南省的GDP总量不超过4000亿元
D.与去年同期相比,2017年第一季度五个省的GDP总量均实现了增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若从第二项起的每一项均大于该项之前的所有项的和,则称
,若从第二项起的每一项均大于该项之前的所有项的和,则称![]() 为
为![]() 数列.
数列.
(1)若![]() 的前
的前![]() 项和
项和![]() ,试判断
,试判断![]() 是否是
是否是![]() 数列,并说明理由;
数列,并说明理由;
(2)设数列![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列,若该数列是
的等差数列,若该数列是![]() 数列,求
数列,求![]() 的取值范围;
的取值范围;
(3)设无穷数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的等比数列,有穷数列
的等比数列,有穷数列![]() ,
,![]() 是从
是从![]() 中取出部分项按原来的顺序所组成的不同数列,其所有项和分别为
中取出部分项按原来的顺序所组成的不同数列,其所有项和分别为![]() ,
,![]() ,求
,求![]() 是
是![]() 数列时
数列时![]() 与
与![]() 所满足的条件,并证明命题“若
所满足的条件,并证明命题“若![]() 且
且![]() ,则
,则![]() 不是
不是![]() 数列”.
数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选题)下列说法中,正确的命题是( )
A.已知随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() .
.
B.以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
C.已知两个变量具有线性相关关系,其回归直线方程为![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
D.若样本数据![]() ,
,![]() ,…,
,…,![]() 的方差为2,则数据
的方差为2,则数据![]() ,
,![]() ,…,
,…,![]() 的方差为16.
的方差为16.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上的点,过
上的点,过![]() 三点的平面与
三点的平面与![]() 交于点
交于点![]() .将①
.将①![]() ,②
,②![]() ,③
,③![]() 中的两个补充到已知条件中,解答下列问题:
中的两个补充到已知条件中,解答下列问题:
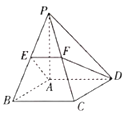
(1)求平面![]() 将四棱锥分成两部分的体积比;
将四棱锥分成两部分的体积比;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系;曲线C1的普通方程为(x-1)2 +y2 =1,曲线C2的参数方程为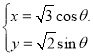 (θ为参数).
(θ为参数).
(Ⅰ)求曲线C1和C2的极坐标方程:
(Ⅱ)设射线θ=![]() (ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
(ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 为椭圆上一动点(异于左右顶点),
为椭圆上一动点(异于左右顶点),![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 两点,问
两点,问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府为了对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房的心理预期调研,用简单随机抽样的方法抽取110人进行统计,得到如图列联表,已知样本中城市人数与农村人数之比是![]() ;
;
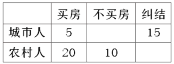
(Ⅰ)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(Ⅱ)请完成列联表,并用独立性检验的思想方法说明有多少的把握认为不买房心理预期与城乡有关?
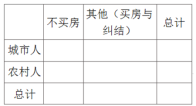
参考公式: ,
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com