【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点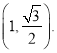
(1)求E的方程;
(2)若直线![]() 与E相交于
与E相交于![]() 两点,且
两点,且![]() 与
与![]() (
(![]() 为坐标原点)的斜率之和为2,求点
为坐标原点)的斜率之和为2,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析: (1)由离心率为![]() ,且过点
,且过点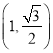 ,可求得椭圆方程; (2)联立直线l与椭圆方程,写出韦达定理,由已知
,可求得椭圆方程; (2)联立直线l与椭圆方程,写出韦达定理,由已知![]() 转化为坐标形式,转化为m与k的等式,再根据点线距公式以及参数的范围求出
转化为坐标形式,转化为m与k的等式,再根据点线距公式以及参数的范围求出![]() 到直线
到直线![]() 距离的取值范围.
距离的取值范围.
试题解析:解:(1)由已知得![]() ,
,
解得![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() ;
;
(2)把![]() 代入
代入![]() 的方程得:
的方程得:
![]() ,
,
其判别式![]() ,①
,①
设![]() ,则
,则![]() ,②
,②
由已知得![]() ,
,
∴![]() ,③
,③
把②代入③得![]() ,
,
即![]() ,④
,④
把④代入①及![]() 知
知![]() ,
,
又![]() ,∴
,∴![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, 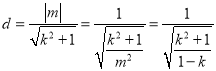 ,
,
令![]() ,则
,则 ,
,
设![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 单调递减,
单调递减,
∴当![]() 时,
时, ![]() ,
,
综上,点![]() 到直线
到直线![]() 的距离的取值范围为
的距离的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
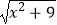 ,g(x)=ax﹣3.
,g(x)=ax﹣3.
(1)当a=l时,确定函数h(x)=f(x)﹣g(x)在(0,+∞)上的单调性;
(2)若对任意x∈[0,4],总存在x0∈[﹣2,2],使得g(x0)=f(x)成立,求 实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某印刷厂为了研究印刷单册书籍的成本
 (单位:元)与印刷册数
(单位:元)与印刷册数 (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:印刷册数
 (千册)
(千册)2
3
4
5
8
单册成本
 (元)
(元)3.2
2.4
2
1.9
1.7
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:
 ,方程乙:
,方程乙:  .
.(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
印刷册数
 (千册)
(千册)2
3
4
5
8
单册成本
 (元)
(元)3.2
2.4
2
1.9
1.7
模型甲
估计值

2.4
2.1
1.6
残差

0
-0.1
0.1
模型乙
估计值

2.3
2
1.9
残差

0.1
0
0
②分别计算模型甲与模型乙的残差平方和
 及
及 ,并通过比较
,并通过比较 ,
,  的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为8千册(概率0.8)或10千册(概率0.2),若印刷厂以每册5元的价格将书籍出售给订货商,问印刷厂二次印刷8千册还是10千册能获得更多利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中
 表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.
表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.
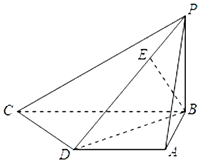
(1)求异面直线PA与CD所成的角的大小;
(2)求证:BE⊥平面PCD;
(3)求二面角A﹣PD﹣B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S. ①当
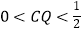 时,S为四边形
时,S为四边形
②截面在底面上投影面积恒为定值
③不存在某个位置,使得截面S与平面A1BD垂直
④当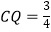 时,S与C1D1的交点满足C1R1=
时,S与C1D1的交点满足C1R1= 
其中正确命题的个数为 ( )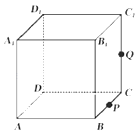
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】第96届(春季)全国糖酒商品交易会于2017年3月23日至25日在四川举办.展馆附近一家川菜特色餐厅为了研究参会人数与本店所需原材料数量的关系,在交易会前查阅了最近5次交易会的参会人数
 (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量 (袋),得到如下数据:
(袋),得到如下数据:
(Ⅰ)请根据所给五组数据,求出
 关于
关于 的线性回归方程
的线性回归方程 ;
;(Ⅱ)若该店现有原材料12袋,据悉本次交易会大约有13万人参加,为了保证原材料能够满足需要,则该店应至少再补充原材料多少袋?
(参考公式:
 ,
,  )
)
相关试题

