【题目】已知函数f(x)= ![]() ,g(x)=ax﹣3.
,g(x)=ax﹣3.
(1)当a=l时,确定函数h(x)=f(x)﹣g(x)在(0,+∞)上的单调性;
(2)若对任意x∈[0,4],总存在x0∈[﹣2,2],使得g(x0)=f(x)成立,求 实数a的取值范围.
参考答案:
【答案】
(1)解:由题意:当a=l时,确定函数h(x)=f(x)﹣g(x)=)= ![]() ﹣x+3.
﹣x+3.
∵x∈(0,+∞)
则 ![]() =
= ![]() >0,
>0,
∴h(x)在(0,+∞)上是单调增函数
(2)解:由题意:x∈[0,4]上函数f(x)= ![]() 的值域M=[3,5],
的值域M=[3,5],
设函数g(x)=ax﹣3的值域N.
∵x0∈[﹣2,2],g(x)=ax﹣3.
当a=0时,g(x)=﹣3,即值域N={﹣3},
∵MN,
∴不满足题意.
当a>0时,函数g(x)在定义域内为增函数,其值域N=[﹣2a﹣3,2a﹣3],
∵MN,
∴需满足 ![]() ,
,
解得:a≥4.
当a<0时,函数g(x)在定义域内为减函数,其值域N=[2a﹣3,﹣2a﹣3],
∵MN,
∴需满足 ![]()
解得:a≤﹣4.
综上所得:对任意x∈[0,4],总存在x0∈[﹣2,2],使得g(x0)=f(x)成立,
实数a的取值范围是(﹣∞,﹣4]∪[4,+∞)
【解析】(1)由题意:当a=l时,确定函数h(x)=f(x)﹣g(x)=)= ![]() ﹣x+3.判断x在(0,+∞)上
﹣x+3.判断x在(0,+∞)上 ![]() 与x的大小可得单调性.(2)求解x∈[0,4]上函数f(x)=
与x的大小可得单调性.(2)求解x∈[0,4]上函数f(x)= ![]() 的值域M,x0∈[﹣2,2]上,对a讨论函数g(x)=ax﹣3的值域N,
的值域M,x0∈[﹣2,2]上,对a讨论函数g(x)=ax﹣3的值域N,
根据MN,可得实数a的取值范围.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)五边形
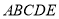 中,
中, 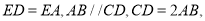
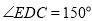 ,将
,将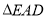 沿
沿 折到
折到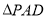 的位置,得到四棱锥
的位置,得到四棱锥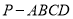 ,如图(2),点
,如图(2),点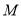 为线段
为线段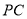 的中点,且
的中点,且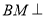 平面
平面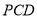 .
.(1)求证:平面
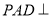 平面
平面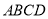 ;
;(2)若直线
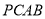 与所成角的正切值为
与所成角的正切值为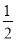 ,求直线
,求直线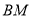 与平面
与平面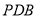 所成角的正弦值.
所成角的正弦值.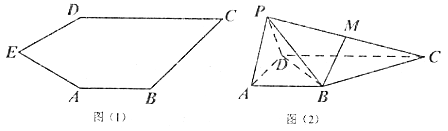
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
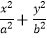 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 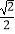 ,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为
,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为 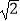 +1 (Ⅰ)求椭圆C的方程;
+1 (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线L的斜率为k,且过左焦点F1 , 与椭圆C相交于P、Q两点,若△PQF2的面积为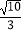 ,试求k的值及直线L的方程.
,试求k的值及直线L的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年入秋以来,某市多有雾霾天气,空气污染较为严重.市环保研究所对近期每天的空气污染情况进行调査研究后发现,每一天中空气污染指数与f(x)时刻x(时)的函数关系为f(x)=|log25(x+1)﹣a|+2a+1,x∈[0,24],其中a为空气治理调节参数,且a∈(0,1).
(1)若a= ,求一天中哪个时刻该市的空气污染指数最低;
,求一天中哪个时刻该市的空气污染指数最低;
(2)规定每天中f(x)的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过3,则调节参数a应控制在什么范围内? -
科目: 来源: 题型:
查看答案和解析>>【题目】某印刷厂为了研究印刷单册书籍的成本
 (单位:元)与印刷册数
(单位:元)与印刷册数 (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:印刷册数
 (千册)
(千册)2
3
4
5
8
单册成本
 (元)
(元)3.2
2.4
2
1.9
1.7
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:
 ,方程乙:
,方程乙:  .
.(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
印刷册数
 (千册)
(千册)2
3
4
5
8
单册成本
 (元)
(元)3.2
2.4
2
1.9
1.7
模型甲
估计值

2.4
2.1
1.6
残差

0
-0.1
0.1
模型乙
估计值

2.3
2
1.9
残差

0.1
0
0
②分别计算模型甲与模型乙的残差平方和
 及
及 ,并通过比较
,并通过比较 ,
,  的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为8千册(概率0.8)或10千册(概率0.2),若印刷厂以每册5元的价格将书籍出售给订货商,问印刷厂二次印刷8千册还是10千册能获得更多利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中
 表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.
表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
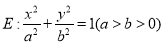 的离心率为
的离心率为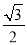 ,且过点
,且过点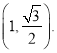
(1)求E的方程;
(2)若直线
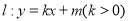 与E相交于
与E相交于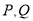 两点,且
两点,且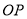 与
与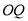 (
(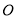 为坐标原点)的斜率之和为2,求点
为坐标原点)的斜率之和为2,求点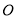 到直线
到直线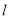 的距离的取值范围.
的距离的取值范围.
相关试题

