【题目】已知函数 ![]() 的部分图象如图所示.
的部分图象如图所示. 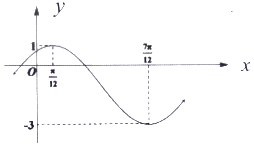
(1)求f(x)的解析式;
(2)求f(x)的单调递增区间和对称中心坐标;
(3)将f(x)的图象向左平移 ![]() 个单位,再讲横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数g(x)的图象,求函数y=g(x)在
个单位,再讲横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数g(x)的图象,求函数y=g(x)在 ![]() 上的最大值和最小值.
上的最大值和最小值.
参考答案:
【答案】
(1)解:由图象可知 ![]() ,可得:A=2,B=﹣1,
,可得:A=2,B=﹣1,
又由于 ![]() =
= ![]() ﹣
﹣ ![]() ,可得:T=π,所以
,可得:T=π,所以 ![]() ,
,
由图象及五点法作图可知:2× ![]() +φ=
+φ= ![]() ,所以φ=
,所以φ= ![]() ,
,
所以f(x)=2sin(2x+ ![]() )﹣1
)﹣1
(2)解:由(1)知,f(x)=2sin(2x+ ![]() )﹣1,
)﹣1,
令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
所以f(x)的单调递增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z,
],k∈Z,
令2x+ ![]() =kπ,k∈Z,得x=
=kπ,k∈Z,得x= ![]() ﹣
﹣ ![]() ,k∈Z,
,k∈Z,
所以f(x)的对称中心的坐标为( ![]() ﹣
﹣ ![]() ,﹣1),k∈Z
,﹣1),k∈Z
(3)解:由已知的图象变换过程可得:g(x)=2sin(x+ ![]() ),
),
因为0≤x≤ ![]() ,所以
,所以 ![]()
![]() ≤
≤ ![]() ,
,
所以当x+ ![]() =
= ![]() ,得x=
,得x= ![]() 时,g(x)取得最小值g(
时,g(x)取得最小值g( ![]() )=﹣2,
)=﹣2,
当x+ ![]() =
= ![]() ,即x=0时,g(x)取得最大值g(0)=
,即x=0时,g(x)取得最大值g(0)= ![]()
【解析】(1)由图象可求A,B,T,利用周期公式可得 ![]() ,由图象及五点法作图可求φ,即可得解f(x)的函数解析式.(2)令2kπ﹣
,由图象及五点法作图可求φ,即可得解f(x)的函数解析式.(2)令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,解得kπ﹣
,k∈Z,解得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,可得f(x)的单调递增区间,令2x+
,k∈Z,可得f(x)的单调递增区间,令2x+ ![]() =kπ,k∈Z,可求f(x)的对称中心的坐标.(3)由已知的图象变换过程可得:g(x)=2sin(x+
=kπ,k∈Z,可求f(x)的对称中心的坐标.(3)由已知的图象变换过程可得:g(x)=2sin(x+ ![]() ),结合范围0≤x≤
),结合范围0≤x≤ ![]() ,可求
,可求 ![]()
![]() ≤
≤ ![]() ,利用正弦函数的图象和性质即可计算得解.
,利用正弦函数的图象和性质即可计算得解.
【考点精析】解答此题的关键在于理解三角函数的最值的相关知识,掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值
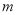
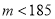
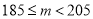
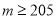
等级
三等品
二等品
一等品
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
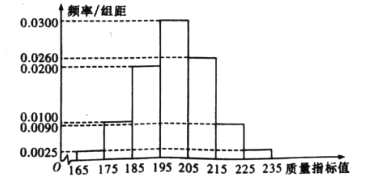
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值
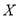 近似满足
近似满足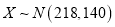 ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为
 +
+ =1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点;若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为________.
=1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点;若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过原点的动直线
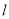 与圆
与圆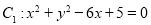 相交于不同的两点
相交于不同的两点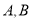 .
.(1)求线段
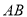 的中点
的中点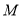 的轨迹
的轨迹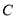 的方程;
的方程;(2)是否存在实数
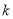 ,使得直线
,使得直线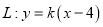 与曲线
与曲线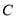 只有一个交点?若存在,求出
只有一个交点?若存在,求出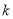 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
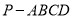 的底面
的底面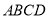 是平行四边形,侧面
是平行四边形,侧面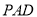 是边长为2的正三角形,
是边长为2的正三角形, 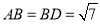 ,
, 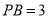 .
.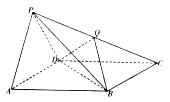
(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)设
 是棱
是棱 上的点,当
上的点,当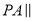 平面
平面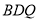 时,求二面角
时,求二面角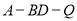 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an},满足a1=1,
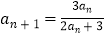 ,n∈N* . (Ⅰ)求证:数列
,n∈N* . (Ⅰ)求证:数列 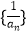 为等差数列;
为等差数列;
(Ⅱ)设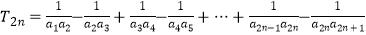 ,求T2n .
,求T2n . -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学考试中,第22题和第23题为选做题,规定每位考生必须且只须在其中选做一题,现有甲、乙、丙、丁4名考生参加考试,其中甲、乙选做第22题的概率均为
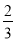 ,丙、丁选做第22题的概率均为
,丙、丁选做第22题的概率均为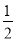 .
.(Ⅰ)求在甲选做第22题的条件下,恰有两名考生选做同一道题的概率;
(Ⅱ)设这4名考生中选做第22题的学生个数为X,求X的概率分布及数学期望.
相关试题

