【题目】已知数列{an},满足a1=1, ![]() ,n∈N* . (Ⅰ)求证:数列
,n∈N* . (Ⅰ)求证:数列 ![]() 为等差数列;
为等差数列;
(Ⅱ)设 ![]() ,求T2n .
,求T2n .
参考答案:
【答案】证明(Ⅰ):法一:由 ![]() ,得
,得 ![]() =
= ![]() =
= ![]() +
+ ![]() , ∴
, ∴ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴数列{ ![]() }是首项为1,公差为
}是首项为1,公差为 ![]() 的等差数列,
的等差数列,
法二:由 ![]() ,得
,得 ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =(
=( ![]() +
+ ![]() )﹣
)﹣ ![]() =
= ![]()
∴数列{ ![]() }是首项为1,公差为
}是首项为1,公差为 ![]() 的等差数列,
的等差数列,
(Ⅱ)解:设bn= ![]() ﹣
﹣ ![]() =(
=( ![]() ﹣
﹣ ![]() )
) ![]() ,
,
由(Ⅰ)得,数列{ ![]() }是首项为1,公差为
}是首项为1,公差为 ![]() 的等差数列,
的等差数列,
∴ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ,
,
即bn=( ![]() ﹣
﹣ ![]() )
) ![]() =﹣
=﹣ ![]() ﹣
﹣ ![]() ,
,
∴bn+1﹣bn=﹣ ![]() (
( ![]() ﹣
﹣ ![]() )=﹣
)=﹣ ![]() ×
× ![]() =﹣
=﹣ ![]() ,
,
且b1=﹣ ![]() ×
× ![]() =﹣
=﹣ ![]() (
( ![]() +
+ ![]() )=﹣
)=﹣ ![]()
∴{bn}是首项b1=﹣ ![]() ,公差为﹣
,公差为﹣ ![]() 的等差数列,
的等差数列,
∴T2n=b1+b2+…+bn=﹣ ![]() n+
n+ ![]() ×(﹣
×(﹣ ![]() )=﹣
)=﹣ ![]() (2n2+3n)
(2n2+3n)
【解析】(Ⅰ)方法一:根据数列的递推公式得到 ![]() =
= ![]() =
= ![]() +
+ ![]() ,即可得到
,即可得到 ![]() ﹣
﹣ ![]() =
= ![]() ,问题得以解决,方法二:根据数列的递推公式得
,问题得以解决,方法二:根据数列的递推公式得 ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =(
=( ![]() +
+ ![]() )﹣
)﹣ ![]() =
= ![]() ,问题得以解决,(Ⅱ)设bn=
,问题得以解决,(Ⅱ)设bn= ![]() ﹣
﹣ ![]() =(
=( ![]() ﹣
﹣ ![]() )
) ![]() ,得到{bn}是首项b1=﹣
,得到{bn}是首项b1=﹣ ![]() ,公差为﹣
,公差为﹣ ![]() 的等差数列,再根据等差数列的求和公式计算即可.
的等差数列,再根据等差数列的求和公式计算即可.
【考点精析】利用等差关系的确定和数列的前n项和对题目进行判断即可得到答案,需要熟知如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系
)那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系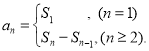 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过原点的动直线
 与圆
与圆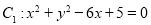 相交于不同的两点
相交于不同的两点 .
.(1)求线段
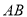 的中点
的中点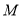 的轨迹
的轨迹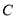 的方程;
的方程;(2)是否存在实数
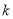 ,使得直线
,使得直线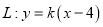 与曲线
与曲线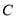 只有一个交点?若存在,求出
只有一个交点?若存在,求出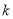 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
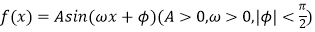 的部分图象如图所示.
的部分图象如图所示. 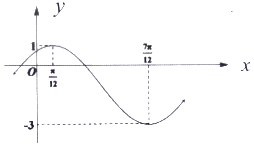
(1)求f(x)的解析式;
(2)求f(x)的单调递增区间和对称中心坐标;
(3)将f(x)的图象向左平移 个单位,再讲横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数g(x)的图象,求函数y=g(x)在
个单位,再讲横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数g(x)的图象,求函数y=g(x)在 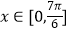 上的最大值和最小值.
上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
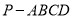 的底面
的底面 是平行四边形,侧面
是平行四边形,侧面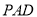 是边长为2的正三角形,
是边长为2的正三角形, 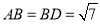 ,
, 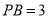 .
.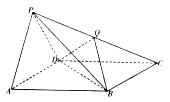
(Ⅰ)求证:平面
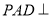 平面
平面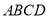 ;
;(Ⅱ)设
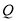 是棱
是棱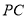 上的点,当
上的点,当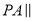 平面
平面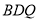 时,求二面角
时,求二面角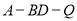 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学考试中,第22题和第23题为选做题,规定每位考生必须且只须在其中选做一题,现有甲、乙、丙、丁4名考生参加考试,其中甲、乙选做第22题的概率均为
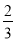 ,丙、丁选做第22题的概率均为
,丙、丁选做第22题的概率均为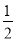 .
.(Ⅰ)求在甲选做第22题的条件下,恰有两名考生选做同一道题的概率;
(Ⅱ)设这4名考生中选做第22题的学生个数为X,求X的概率分布及数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若圆
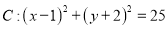 上有四个不同的点到直线
上有四个不同的点到直线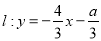 的距离为2,则
的距离为2,则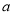 的取值范围是( )
的取值范围是( )A. (-12,8) B. (-8,12) C. (-13,17) D. (-17,13)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
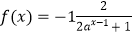 (a>0且a≠1)是定义在R上的奇函数. (Ⅰ) 求实数a的值;
(a>0且a≠1)是定义在R上的奇函数. (Ⅰ) 求实数a的值;
(Ⅱ) 证明函数f(x)在R上是增函数;
(Ⅲ)当x∈[1,+∞)时,mf(x)≤2x﹣2恒成立,求实数m的取值范围.
相关试题

