【题目】已知函数![]() 在区间
在区间![]() 上有最大值
上有最大值![]() 和最小值
和最小值![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() ,
,
证明:对任意实数![]() ,函数
,函数![]() 的图象与直线
的图象与直线![]() 最多只有一个交点;
最多只有一个交点;
(3)设![]() ,是否存在实数m和n
,是否存在实数m和n![]() m<n
m<n![]() ,使
,使![]() 的定义域和值域分别为
的定义域和值域分别为![]() ,如果存在,求出m和n的值.若不存在,请说明理由。
,如果存在,求出m和n的值.若不存在,请说明理由。
参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)由题意得到函数![]() 在区间
在区间![]() 上单调递增,结合题意可求得
上单调递增,结合题意可求得![]() .(2)由
.(2)由![]() 得
得![]() ,构造函数
,构造函数![]() ,可证明函数
,可证明函数![]() 单调递增,故得结论成立.(3)分析条件可得函数
单调递增,故得结论成立.(3)分析条件可得函数![]() 在
在![]() 上单调递增,于是可得到
上单调递增,于是可得到![]() ,于是得
,于是得![]() 为方程
为方程![]() 的两个不等实根,解方程可得
的两个不等实根,解方程可得![]() .
.
(1)由题意得![]() ,
,
∴函数![]() 图象的对称轴为
图象的对称轴为![]() ,
,
∴函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
由题得![]() ,
,
解得![]() .
.
(2)证明:由(1)知![]() ,
,
∴![]() ,
,
令![]() ,
,
∴![]() ,
,
令![]() .
.
设![]() ,则
,则![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴函数![]() 为
为![]() 上的增函数,
上的增函数,
∴对任意实数![]() ,函数
,函数![]() 的图象与直线
的图象与直线![]() 最多只有一个交点.
最多只有一个交点.
(3)由题意知![]() ,对称轴为
,对称轴为![]() ,
,
∴![]() .
.
假设存在实数![]() ,使得当
,使得当![]() 时,
时,![]() 的值域为
的值域为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
则![]() 为方程
为方程![]() 的两个不等实根,
的两个不等实根,
由![]() 得
得![]() ,
,
解得![]() ,
,![]() .经检验得满足条件.
.经检验得满足条件.
故存在![]() ,
,![]() 使得
使得![]() 的定义域和值域分别为
的定义域和值域分别为![]() .
.
-
科目: 来源: 题型:
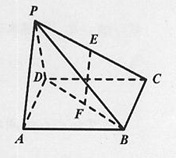
查看答案和解析>>【题目】如图,在四棱锥
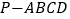 中,底面
中,底面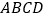 是边长为2的正方形,
是边长为2的正方形,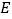 ,
,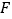 分别为
分别为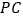 ,
,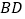 的中点,平面
的中点,平面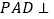 平面
平面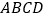 ,且
,且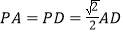 .
.
(1)求证:
 平面
平面 ;
;(2)求三棱锥
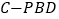 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  的左右焦点分别
的左右焦点分别
 ,过
,过 作垂直于
作垂直于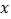 轴的直线
轴的直线 交椭圆于
交椭圆于 两点,满足
两点,满足 .
.(1)求椭圆
 的离心率.
的离心率.(2)
 是椭圆
是椭圆 短轴的两个端点,设点
短轴的两个端点,设点 是椭圆
是椭圆 上一点(异于椭圆
上一点(异于椭圆 的顶点),直线
的顶点),直线 分别与
分别与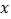 轴相交于
轴相交于 两点,
两点, 为坐标原点,若
为坐标原点,若 ,求椭圆
,求椭圆 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=e|lnx|(e为自然对数的底数).若x1≠x2且f(x1)=f(x2),则下列结论一定不成立的是( )
A.x2f(x1)>1
B.x2f(x1)=1
C.x2f(x1)<1
D.x2f(x1)<x1f(x2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则b+c的取值范围为( )
,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则b+c的取值范围为( )
A.(﹣∞,3)
B.(0,3]
C.[0,3]
D.(0,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知曲线C1:
 , 曲线C2:
, 曲线C2: ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. 并在两种坐标系中取相同的单位长度。
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. 并在两种坐标系中取相同的单位长度。(1)写出曲线C1,C2的极坐标方程;
(2)在极坐标系中,已知点A是射线l:
 与C1的交点,点B是l与C2的异于极点的交点,当
与C1的交点,点B是l与C2的异于极点的交点,当 在区间
在区间 上变化时,求
上变化时,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,CA=CB=2,M,N是斜边AB上的两个动点,且MN=
 ,则
,则 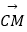
 的取值范围为 .
的取值范围为 .
相关试题

