【题目】关于x的实系数一元二次方程![]() 有两个异号实根的充要条件是什么?为什么?
有两个异号实根的充要条件是什么?为什么?
参考答案:
【答案】【解答】关于x的实系数的一元二次方程![]() 有两个异号实根的充要条件是ac<0.
有两个异号实根的充要条件是ac<0.
证明:①充分性:∵ac<0,∴-4ac>0,∴Δ=b2-4ac>0,∴设x1 , x2为原方程的两个不等实根,又由根与系数的关系得![]() 则x1,x2异号,即ac<0是关于x的实系数一元二次方程ax2+bx+c=0有两个异号实根的充分条件.
则x1,x2异号,即ac<0是关于x的实系数一元二次方程ax2+bx+c=0有两个异号实根的充分条件.
②必要性;设x1 , x2是关于x的实系数一元二次方程ax2+bx+c=0的两个实根异号,则![]() ,所以ac<0,即ac<0是关于x的系数的一元 二次方程ax2+bx+c=0有两个异号实根的必要条件.综合(1)(2)可得原结论成立
,所以ac<0,即ac<0是关于x的系数的一元 二次方程ax2+bx+c=0有两个异号实根的必要条件.综合(1)(2)可得原结论成立
【解析】证明充要条件,首先证明充分性,再证明必要性,最后总结即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)为奇函数,当x≥0时,f(x)=
 .g(x)=
.g(x)=  ,
,
(1)求当x<0时,函数f(x)的解析式,并在给定直角坐标系内画出f(x)在区间[﹣5,5]上的图象;(不用列表描点)
(2)根据已知条件直接写出g(x)的解析式,并说明g(x)的奇偶性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知条件p:-1≤x≤10,q:x2-4x+4-m2≤0(m>0)不变,若
 p是
p是  q的必要而不充分条件,如何求实数m的取值范围?
q的必要而不充分条件,如何求实数m的取值范围? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式x2﹣(a2+3a+2)x+3a(a2+2)<0(a∈R).
(Ⅰ)解该不等式;
(Ⅱ)定义区间(m,n)的长度为d=n﹣m,若a∈R,求该不等式解集表示的区间长度的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,判断条件p是条件q的什么条件:
(1)p:|x|=|y|,q:x=y;
(2)p:△ABC是直角三角形,q:△ABC是等腰三角形;
(3)p:四边形的对角线互相平分,q:四边形是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.命题“若x2>1,则x>1”的否命题为“若x2>1,则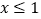 ”
”
B.命题“?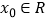 ,x>1”的否定是“
,x>1”的否定是“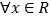 ,x2>1”
,x2>1”
C.命题“若x=y,则cosx=cosy"的逆否命题为假命题
D.命题“若x=y,则cosx=cosy"的逆命题为假命题 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中的真命题是( )
A.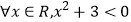
B.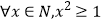
C. 使x5<1
使x5<1
D.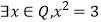
相关试题

