【题目】下列函数中的奇函数是( )
A.f(x)=x+1
B.f(x)=3x2﹣1
C.f(x)=2(x+1)3﹣1
D.f(x)═﹣ ![]()
参考答案:
【答案】D
【解析】解:A.f(x)=x+1,f(﹣x)=﹣x+1,不满足f(﹣x)=﹣f(x),不为奇函数;
B.f(x)=3x2﹣1,f(﹣x)=3(﹣x)2﹣1=f(x),f(x)为偶函数;
C.f(x)=2(x+1)3﹣1,f(﹣x)=2(﹣x+1)3﹣1,不满足f(﹣x)=﹣f(x),不为奇函数;
D.f(x)═﹣ ![]() ,f(﹣x)═
,f(﹣x)═ ![]() =﹣f(x),则f(x)为奇函数.
=﹣f(x),则f(x)为奇函数.
故选:D.
【考点精析】根据题目的已知条件,利用函数的奇偶性的相关知识可以得到问题的答案,需要掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在函数
 (
( )的所有切线中,有且仅有一条切线
)的所有切线中,有且仅有一条切线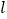 与直线
与直线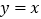 垂直.
垂直.(1)求
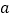 的值和切线
的值和切线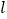 的方程;
的方程;(2)设曲线
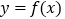 在任一点处的切线倾斜角为
在任一点处的切线倾斜角为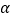 ,求
,求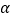 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳
不喜欢游泳
合计
男生
10
女生
20
合计
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为
 .
.(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:

0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:
 ,其中
,其中 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
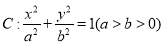 的离心率为
的离心率为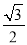 ,且过点
,且过点 .
.(Ⅰ)求椭圆
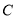 的方程.
的方程.(Ⅱ)若
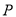 ,
, 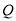 是椭圆
是椭圆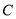 上两个不同的动点,且使
上两个不同的动点,且使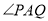 的角平分线垂直于
的角平分线垂直于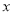 轴,试判断直线
轴,试判断直线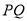 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a=log36,a=log510,a=log714,则( )
A.a>b>c
B.a>c>b
C.c>a>b
D.c>b>a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形
 中,
中, 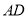 //
// 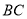 ,
, 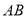 ⊥
⊥ ,
, 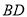 ⊥
⊥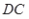 , 点
, 点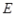 是
是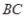 边的中点, 将△
边的中点, 将△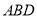 沿
沿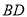 折起,使平面
折起,使平面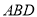 ⊥平面
⊥平面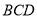 ,连接
,连接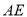 ,
, 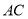 ,
, 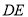 , 得到如
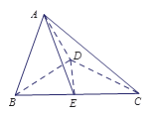
, 得到如图所示的空间几何体.
(Ⅰ)求证:
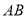 ⊥平面
⊥平面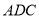 ;
;(Ⅱ)若
 ,求点
,求点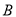 到平面
到平面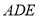 的距离.
的距离.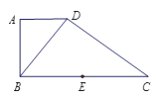
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知函数
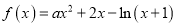 (a为常数).
(a为常数).(Ⅰ)当
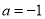 时,求函数
时,求函数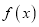 的单调区间;
的单调区间;(Ⅱ)当
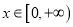 时,不等式
时,不等式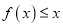 恒成立,求实数
恒成立,求实数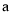 的取值范围.
的取值范围.
相关试题

