【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,得曲线
轴的正半轴为极轴建立极坐标系,得曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() .
.
(1)化曲线![]() 的参数方程为普通方程,化曲线
的参数方程为普通方程,化曲线![]() 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;
(2)直线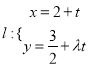 (
(![]() 为参数)过曲线
为参数)过曲线![]() 与
与![]() 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线![]() 平行且与曲线
平行且与曲线![]() 相切的直线方程.
相切的直线方程.
参考答案:
【答案】(Ⅰ)![]() 、
、![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]()
【解析】试题分析:(1)利用![]() 将极坐标方程转化为直角坐标方程
将极坐标方程转化为直角坐标方程![]() ,利用平方消元法将参数方程化为普通方程
,利用平方消元法将参数方程化为普通方程![]() ,(2)先根据直线
,(2)先根据直线![]() 过
过![]() 得
得![]() ,再利用代入消元将参数方程化为普通方程
,再利用代入消元将参数方程化为普通方程![]() ,可设与直线
,可设与直线![]() 平行且与曲线
平行且与曲线![]() 相切的直线方程为:
相切的直线方程为: ![]() ,最后根据圆心到切线距离等于半径求
,最后根据圆心到切线距离等于半径求![]() 或
或![]()
试题解析:(Ⅰ)曲线![]() 的普通方程为:
的普通方程为: ![]()
由![]() 得
得![]() ,
,
∴曲线![]() 的直角坐标方程为:
的直角坐标方程为: ![]()
(或:曲线![]() 的直角坐标方程为:
的直角坐标方程为: ![]() )
)
(Ⅱ)曲线![]() :
: ![]() 与
与![]() 轴负半轴的交点坐标为
轴负半轴的交点坐标为![]() ,
,
又直线![]() 的参数方程为:
的参数方程为: 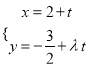 ,∴
,∴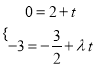 ,得
,得![]() ,
,
即直线![]() 的参数方程为:
的参数方程为: 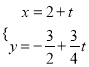
得直线![]() 的普通方程为:
的普通方程为: ![]() ,
,
设与直线![]() 平行且与曲线
平行且与曲线![]() 相切的直线方程为:
相切的直线方程为: ![]()
∵曲线![]() 是圆心为
是圆心为![]() ,半径为5的圆,
,半径为5的圆,
得![]() ,解得
,解得![]() 或
或![]()
故所求切线方程为: ![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇,2016年双11期间,某平台的销售业绩高达918亿人民币,与此同时,相关管理部门也推出了针对电商的商品和服务评价体系,现从评价系统中随机选出200次成功的交易,并对其评价结果进行统计,对商品的好评率为
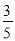 ,对服务的好评率为
,对服务的好评率为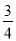 ,其中对商品和服务都做出好评的交易为80次.
,其中对商品和服务都做出好评的交易为80次.在犯错误概率不超过( )的前提下,认为商品好评与服务好评有关.
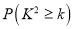
0.15
0.10
0.05
0.025
0.010
0.005
0.001
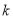
2.072
2.706
3.841
5.024
6.635
7.879
10.828
A.
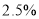 B.
B. 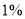 C.
C. 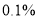 D.
D. 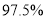
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
 .
.(1)当
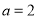 时,解不等式
时,解不等式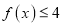 ;
;(2)若
 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,
中,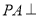 底面
底面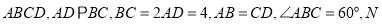 为线段
为线段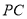 上一点,
上一点,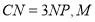 为
为 的中点.
的中点. 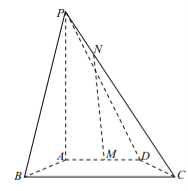
(1)证明:
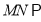 平面
平面 ;
;(2)求点
 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合
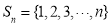 ,若X是
,若X是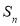 的子集,把X中所有元素的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为
的子集,把X中所有元素的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为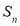 的奇(偶)子集.
的奇(偶)子集.(1)写出S4的所有奇子集;
(2)求证:
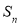 的奇子集与偶子集个数相等;
的奇子集与偶子集个数相等;(3)求证:当n≥3时,
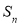 的所有奇子集的容量之和等于所有偶子集的容量之和.
的所有奇子集的容量之和等于所有偶子集的容量之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
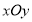 中,曲线
中,曲线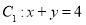 ,曲线
,曲线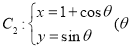 为参数), 以坐标原点
为参数), 以坐标原点 为极点,
为极点,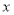 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求曲线
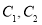 的极坐标方程;
的极坐标方程;(2)若射线
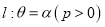 分别交
分别交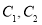 于
于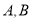 两点, 求
两点, 求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,点
,点 在椭圆
在椭圆 上.
上.(1)求椭圆
 的方程;
的方程;(2)设过点
 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆 于
于 、
、 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 轴交于点
轴交于点 ,求点
,求点 的横坐标的取值范围;
的横坐标的取值范围;(3)在第(2)问的条件下,求
 面积的最大值.
面积的最大值.
相关试题

