【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,且
,且![]() 与抛物线
与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆的标准方程;
(2)若过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,过
两点,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]() ,求
,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)椭圆的标准方程为![]() ;(2)
;(2)![]() 的最小值为
的最小值为![]() .
.
【解析】试题分析:(1)由题可知)抛物线![]() 的焦点为
的焦点为![]() ,所以
,所以![]() ,然后根据离心率可得a值,从而得出椭圆标准方程(2)根据题意则需求出AC和BD的长度表达式,显然可以根据直线与椭圆的弦长公式求得,所以设
,然后根据离心率可得a值,从而得出椭圆标准方程(2)根据题意则需求出AC和BD的长度表达式,显然可以根据直线与椭圆的弦长公式求得,所以设![]() ,
, ![]() ,直线
,直线![]() 的方程为
的方程为![]() ,代入椭圆方程
,代入椭圆方程![]() ,
, ![]() ,同理求出AC的长度,然后化简即得
,同理求出AC的长度,然后化简即得![]()
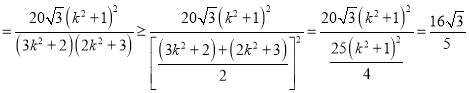 .
.
解析:
(1)抛物线![]() 的焦点为
的焦点为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以椭圆的标准方程为
,所以椭圆的标准方程为![]() .
.
(2)(i)当直线![]() 的斜率
的斜率![]() 存在且
存在且![]() 时,
时,
直线![]() 的方程为
的方程为![]() ,代入椭圆方程
,代入椭圆方程![]() ,
,
并化简得![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
![]()
![]() .
.
易知![]() 的斜率为
的斜率为![]() ,
,
所以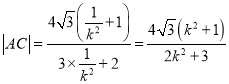 .
.
![]()
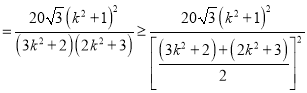
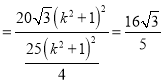 .
.
当![]() ,即
,即![]() 时,上式取等号,故
时,上式取等号,故![]() 的最小值为
的最小值为![]() .
.
(ii)当直线![]() 的斜率不存在或等于零时,易得
的斜率不存在或等于零时,易得![]() .
.
综上, ![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直角坐标系中动点
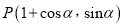 ,参数
,参数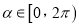 ,在以原点为极点、
,在以原点为极点、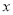 轴正半轴为极轴所建立的极坐标系中,动点
轴正半轴为极轴所建立的极坐标系中,动点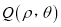 在曲线
在曲线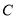 :
: 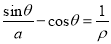 上.
上.(1)求点
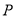 的轨迹
的轨迹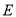 的普通方程和曲线
的普通方程和曲线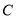 的直角坐标方程;
的直角坐标方程;(2)若动点
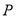 的轨迹
的轨迹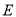 和曲线
和曲线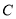 有两个公共点,求实数
有两个公共点,求实数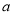 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】现在的人基本每天都离不开手机,许多人手机一旦不在身边就不舒服,几乎达到手机二十四小时不离身,这类人群被称为“手机控”,这一群体在大学生中比较突出.为了调查大学生每天使用手机的时间,某调查公司针对某高校男生、女生各25名学生进行了调查,其中每天使用手机时间超过8小时的被称为:“手机控”,否则被称为“非手机控”.调查结果如下:
手机控
非手机控
合计
女生
5
男生
10
合计
50
(1)将上面的列联表补充完整,再判断是否有99.5%的把握认为“手机控”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“手机控”的人数为
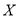 ,试求
,试求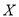 的分布列与数学期望.
的分布列与数学期望.参考公式:
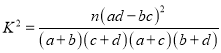 ,其中
,其中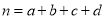 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】棱台
 的三视图与直观图如图所示.
的三视图与直观图如图所示.
(1)求证:平面
 平面
平面 ;
;(2)在线段
 上是否存在一点
上是否存在一点 ,使
,使 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ?若存在,指出点
?若存在,指出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018天一大联考高中毕业班阶段性测试(四)】已知函数
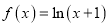 ,
, 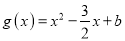 .
.(I)若
 恒成立,求实数
恒成立,求实数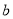 的取值范围;
的取值范围;(II)证明:对于任意正整数
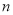 ,都有
,都有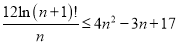 成立.
成立.附:
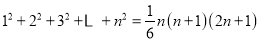 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线
中,曲线 的参数方程是
的参数方程是 (
( 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点,  轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.(1)写出曲线
 的普通方程和直线
的普通方程和直线 的直角坐标方程;
的直角坐标方程;(2)设点
 ,直线
,直线 与曲线
与曲线 相交于
相交于 两点,且
两点,且 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年10月9日,教育部考试中心下发了《关于2017年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.宿州市教育部门积极回应,编辑传统文化教材,在全市范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了200位市民进行了解,发现支持开展的占
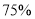 ,在抽取的男性市民120人中持支持态度的为80人.
,在抽取的男性市民120人中持支持态度的为80人.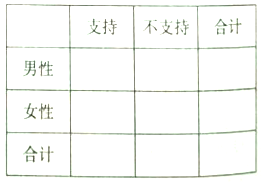
(Ⅰ)完成
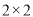 列联表,并判断是否有
列联表,并判断是否有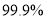 的把握认为性别与支持与否有关?
的把握认为性别与支持与否有关?(Ⅱ)为了进一步征求对开展传统文化的意见和建议,从抽取的200位市民中对不支持的按照分层抽样的方法抽取5位市民,并从抽取的5人中再随机选取2人进行座谈,求选取的2人恰好为1男1女的概率.
附:
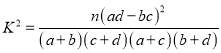 .
.
相关试题

