【题目】已知函数f(x)= ![]() ,
,
(1)若a=﹣1,求f(x)的单调区间;
(2)若f(x)有最大值3,求a的值.
(3)若f(x)的值域是(0,+∞),求a的取值范围.
参考答案:
【答案】
(1)解:当a=﹣1时,f(x)= ![]() ,
,
令g(x)=﹣x2﹣4x+3,
由于g(x)在(﹣∞,﹣2)上单调递增,在(﹣2,+∞)上单调递减,
而y= ![]() t在R上单调递减,
t在R上单调递减,
所以f(x)在(﹣∞,﹣2)上单调递减,在(﹣2,+∞)上 单调递增,
即函数f( x)的递增区间是(﹣2,+∞),递减区间是(﹣∞,﹣2 )
(2)解:令h(x)=ax2﹣4x+3,y= ![]() h(x),由于f(x)有最大值3,
h(x),由于f(x)有最大值3,
所以 h(x)应有最小值﹣1,
因此 ![]() =﹣1,
=﹣1,
解得a=1.
即当f(x)有最大值3时,a的值等于1
(3)解:由指数函数的性质知,
要使y=h(x)的值域为(0,+∞).
应使h(x)=ax2﹣4x+3的值域为R,
因此只能有a=0.
因为若a≠0,则h(x)为二次函数,其值域不可能为R.
故 a的取值范围是{0}
【解析】(1)当a=﹣1时,f(x)= ![]() ,令g(x)=﹣x2﹣4x+3,结合指数函数的单调性,二次函数的单调性和复合函数的单调性,可得f(x)的单调区间;(2)令h(x)=ax2﹣4x+3,y=h(x) , 由于f(x)有最大值3,所以 h(x)应有最小值﹣1,进而可得a的值.(3)由指数函数的性质知,要使y=h(x)的值域为(0,+∞).应使h(x)=ax2﹣4x+3的值域为R , 进而可得a的取值范围.
,令g(x)=﹣x2﹣4x+3,结合指数函数的单调性,二次函数的单调性和复合函数的单调性,可得f(x)的单调区间;(2)令h(x)=ax2﹣4x+3,y=h(x) , 由于f(x)有最大值3,所以 h(x)应有最小值﹣1,进而可得a的值.(3)由指数函数的性质知,要使y=h(x)的值域为(0,+∞).应使h(x)=ax2﹣4x+3的值域为R , 进而可得a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,
 )在椭圆E:
)在椭圆E:  =1上,若斜率为
=1上,若斜率为  的直线l与椭圆E交于B,C两点,当△ABC的面积最大时,求直线l的方程.
的直线l与椭圆E交于B,C两点,当△ABC的面积最大时,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆O:x2+y2=4与x轴相交于A,B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求
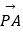
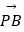 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,b>0,且
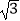 是3a与3b的等比中项,若
是3a与3b的等比中项,若  +
+  ≥2m2+3m恒成立,则实数m的取值范围是 .
≥2m2+3m恒成立,则实数m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos2x+2sin2x+2sinx.
(1)将函数f(2x)的图象向右平移
 个单位得到函数g(x)的图象,若x∈
个单位得到函数g(x)的图象,若x∈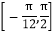 ,求函数g(x)的值域;
,求函数g(x)的值域;(2)已知a,b,c分别为△ABC中角A,B,C的对边,且满足f(A)=
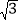 +1,A∈
+1,A∈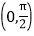 ,a=2
,a=2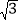 ,b=2,求△ABC的面积.
,b=2,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了检测某种产品的质量(单位:千克),抽取了一个容量为N的样本,整理得到的数据作出了频率分布表和频率分布直方图如图:
分组
频数
频率
[17.5,20)
10
0.05
[20,225)
50
0.25
[22.5,25)
a
b
[25,27.5)
40
c
[27.5,30]
20
0.10
合计
N
1
(Ⅰ)求出表中N及a,b,c的值;
(Ⅱ)求频率分布直方图中d的值;
(Ⅲ)从该产品中随机抽取一件,试估计这件产品的质量少于25千克的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 =1(a>b>0)的左右焦点分别为F1 , F2 , 点
=1(a>b>0)的左右焦点分别为F1 , F2 , 点 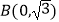 为短轴的一个端点,∠OF2B=60°.
为短轴的一个端点,∠OF2B=60°.
(Ⅰ)求椭圆C的方程;
(Ⅱ)如图,过右焦点F2 , 且斜率为k(k≠0)的直线l与椭圆C相交于D,E两点,A为椭圆的右顶点,直线AE,AD分别交直线x=3于点M,N,线段MN的中点为P,记直线PF2的斜率为k′.试问kk′是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
相关试题

