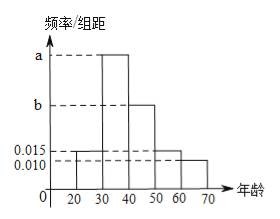
【题目】根据某电子商务平台的调查统计显示,参与调查的![]() 位上网购物者的年龄情况如右图.
位上网购物者的年龄情况如右图.
(1)已知![]() 、
、![]() 、
、![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放![]() 元的代金券,潜在消费人群每人发放
元的代金券,潜在消费人群每人发放![]() 元的代金券.已经采用分层抽样的方式从参与调查的
元的代金券.已经采用分层抽样的方式从参与调查的![]() 位上网购物者中抽取了
位上网购物者中抽取了![]() 人,现在要在这
人,现在要在这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求此三人获得代金券总和
人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
参考答案:
【答案】(1)![]() ;(2)分布列略,186.
;(2)分布列略,186.
【解析】
试题分析:(1)由于五个组的频率之和等于1,即五个矩形的面积之和为1,即求得![]() 的知;
的知;
(2)由已知高消费人群所占比例为![]() ,潜在消费人群的比例为
,潜在消费人群的比例为![]() ,由分层抽样的性质知抽出的
,由分层抽样的性质知抽出的![]() 人中,高消费人群有
人中,高消费人群有![]() 人,潜在消费人群有
人,潜在消费人群有![]() 人,随机抽取的三人中代金券总和
人,随机抽取的三人中代金券总和![]() 可能的取值为:
可能的取值为:![]() ,由离散随机变量概率公式列得分布列,继而求得数学期望.
,由离散随机变量概率公式列得分布列,继而求得数学期望.
试题解析:(1)由于五个组的频率之和等于1,故:
![]() ,
,
又因为![]() 、
、![]() 、
、![]() 三个年龄段的上网购物者人数成等差数列
三个年龄段的上网购物者人数成等差数列
所以![]()
联立解出![]()
(3)由已知高消费人群所占比例为![]() ,潜在消费人群的比例为
,潜在消费人群的比例为![]()
由分层抽样的性质知抽出的![]() 人中,高消费人群有
人中,高消费人群有![]() 人,潜在消费人群有
人,潜在消费人群有![]() 人,
人,
随机抽取的三人中代金券总和![]() 可能的取值为:
可能的取值为:![]()
![]() ;
;![]()
![]() ;
;![]()
列表如下:
|
|
|
|
|
|
|
|
|
|
数学期望![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱柱
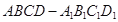 的底面是边长为
的底面是边长为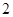 的菱形,且
的菱形,且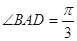 ,
,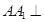 平面
平面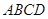 ,
,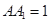 ,设
,设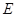 为
为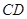 的中点
的中点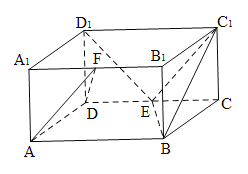
(1)求证:
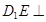 平面
平面
(2)点
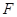 在线段
在线段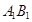 上,且
上,且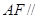 平面
平面 ,求平面
,求平面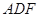 和平面
和平面 所成锐角的余弦值.
所成锐角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
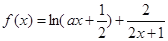
(1)若
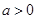 ,且
,且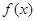 在
在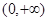 上单调递增,求实数
上单调递增,求实数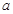 的取值范围
的取值范围(2)是否存在实数
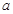 ,使得函数
,使得函数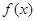 在
在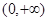 上的最小值为
上的最小值为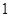 ?若存在,求出实数
?若存在,求出实数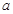 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
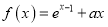 ,
, 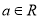 .
.(1)讨论函数
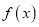 的单调区间;
的单调区间;(2)求证:
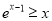 ;
;(3)求证:当
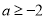 时,
时, 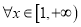 ,
, 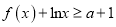 恒成立.
恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
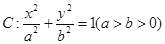 的离心率为
的离心率为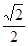 ,椭圆
,椭圆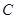 和抛物线
和抛物线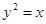 交于
交于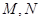 两点,且直线
两点,且直线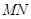 恰好通过椭圆
恰好通过椭圆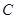 的右焦点.
的右焦点.(1)求椭圆
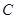 的标准方程;
的标准方程;(2)经过椭圆
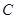 右焦点的直线
右焦点的直线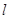 和椭圆
和椭圆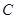 交于
交于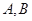 两点,点
两点,点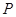 在椭圆上,且
在椭圆上,且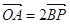 ,
,其中
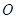 为坐标原点,求直线
为坐标原点,求直线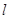 的斜率.
的斜率. -
科目: 来源: 题型:
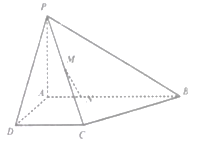
查看答案和解析>>【题目】如图所示,四棱锥
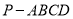 中,四边形
中,四边形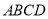 是直角梯形,
是直角梯形, 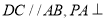 底面
底面 ,
, 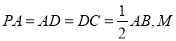 为
为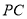 的中点,
的中点,  点在
点在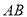 上,且
上,且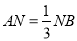 .
.
(1)证明:
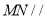 平面
平面 ;
;(2)求直线
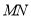 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】重庆市乘坐出租车的收费办法如下:
⑴不超过3千米的里程收费10元;
⑵超过3千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费);
当车程超过3千米时,另收燃油附加费1元.

相应系统收费的程序框图如图所示,其中
 (单位:千米)为行驶里程,
(单位:千米)为行驶里程, (单位:元)为所收费用,用
(单位:元)为所收费用,用 表示不大于
表示不大于 的最大整数,则图中①处应填( )
的最大整数,则图中①处应填( )A.
 B.
B.
C.
 D.
D.
相关试题

