【题目】已知圆C:x2+(y-1)2=5,直线l:mx-y+1-m=0(m∈R).
(1)判断直线l与圆C的位置关系;
(2)设直线l与圆C交于A,B两点,若直线l的倾斜角为120°,求弦AB的长.
参考答案:
【答案】(1)直线l与圆C必相交 (2)![]() .
.
【解析】
(1)判断直线过定点![]() ,利用点与圆的位置关系即可判断直线
,利用点与圆的位置关系即可判断直线![]() 与圆
与圆![]() 的位置关系;(2)根据直线
的位置关系;(2)根据直线![]() 的倾斜角为
的倾斜角为![]() ,求出直线斜率以及直线的方程,利用弦长公式即可求弦
,求出直线斜率以及直线的方程,利用弦长公式即可求弦![]() 的长.
的长.
(1)直线l可变形为y-1=m(x-1),因此直线l过定点D(1,1),
又![]() =1<
=1<![]() ,所以点D在圆C内,则直线l与圆C必相交.
,所以点D在圆C内,则直线l与圆C必相交.
(2)由题意知m≠0,所以直线l的斜率k=m,又k=tan 120°=-![]() ,即m=-
,即m=-![]() .
.
此时,圆心C(0,1)到直线l:![]() x+y-
x+y-![]() -1=0的距离d=
-1=0的距离d=![]() =
=![]() ,
,
又圆C的半径r=![]() ,所以|AB|=2
,所以|AB|=2![]() =2
=2![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的顶点
的顶点 ,
, 边上的中线
边上的中线 所在的直线方程为
所在的直线方程为 ,
, 边上的高
边上的高 所在直线的方程为
所在直线的方程为 .
.(
 )求
)求 的顶点
的顶点 、
、 的坐标.
的坐标.(
 )若圆
)若圆 经过不同的三点
经过不同的三点 、
、 、
、 ,且斜率为
,且斜率为 的直线与圆
的直线与圆 相切于点
相切于点 ,求圆
,求圆 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点的椭圆
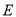 的长轴的一个端点是抛物线
的长轴的一个端点是抛物线 的焦点,且椭圆
的焦点,且椭圆 的离心率是
的离心率是 .
.(1)求椭圆
 的方程;
的方程;(2)过点
 的动直线与椭圆
的动直线与椭圆 相交于
相交于 两点.若线段
两点.若线段 的中点的横坐标是
的中点的横坐标是 ,求直线
,求直线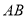 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点
 为圆心的圆经过点
为圆心的圆经过点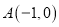 和
和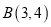 ,线段
,线段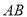 的垂直平分线交圆
的垂直平分线交圆 于点
于点 和
和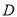 ,且
,且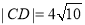 .
.(1)求直线
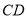 的方程;
的方程;(2)求圆
 的方程;
的方程;(3)设点
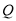 在圆
在圆 上,试问使△
上,试问使△ 的面积等于8的点
的面积等于8的点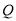 共有几个?证明你的结论.
共有几个?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C1:
 与圆C2:
与圆C2: 相交于A、B两点,
相交于A、B两点,(1)求公共弦AB所在的直线方程;
(2)求圆心在直线
 上,且经过A、B两点的圆的方程.
上,且经过A、B两点的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
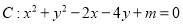
(1)若
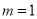 ,过点
,过点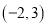 的直线
的直线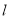 交曲线
交曲线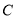 于
于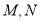 两点,且
两点,且 ,求直线
,求直线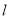 的方程;
的方程;(2)若曲线
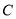 表示圆时,已知圆
表示圆时,已知圆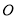 与圆
与圆 交于
交于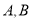 两点,若弦
两点,若弦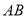 所在的直线方程为
所在的直线方程为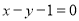 ,
, 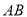 为圆
为圆 的直径,且圆
的直径,且圆 过原点,求实数
过原点,求实数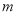 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)满足2x2f(x)+x3f′(x)=ex , f(2)=
 ,则x∈[2,+∞)时,f(x)( )
,则x∈[2,+∞)时,f(x)( )
A.有最大值
B.有最小值
C.有最大值
D.有最小值
相关试题

