【题目】已知曲线![]()
(1)若![]() ,过点
,过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若曲线![]() 表示圆时,已知圆
表示圆时,已知圆![]() 与圆
与圆![]() 交于
交于![]() 两点,若弦
两点,若弦![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 为圆
为圆![]() 的直径,且圆
的直径,且圆![]() 过原点,求实数
过原点,求实数![]() 的值.
的值.
参考答案:
【答案】(1)![]() 或
或![]() (即
(即![]() ) ;(2)
) ;(2) ![]() .
.
【解析】试题分析:(1)由已知条件推导出圆心C(1,2),2为半径,由此利用点到直线的距离公式结合已知条件能求出m=1.
(2)求出圆![]() 的方程,两圆相减得公共弦方程
的方程,两圆相减得公共弦方程![]() ,即得m.
,即得m.
试题解析:
(1) 当![]() 时, 曲线C是以
时, 曲线C是以![]() 为圆心,2为半径的圆,
为圆心,2为半径的圆,
若直线![]() 的斜率不存在,显然不符,
的斜率不存在,显然不符,
故可直线![]() 为:
为: ![]() ,即
,即![]() .
.
由题意知,圆心![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,
,
即: ![]()
解得![]() 或
或![]() .故的方程
.故的方程![]() 或
或![]() (即
(即![]() )
)
(2)由曲线C表示圆![]() ,即
,即![]() ,
,
所以圆心C(1,2),半径![]() ,则必有
,则必有![]() .
.
设过圆心![]() 且与
且与![]() 垂直的直线为:
垂直的直线为: ![]() ,解得
,解得![]() ;
;
![]() ,所以,圆心
,所以,圆心![]()
又因为圆![]() 过原点,则
过原点,则![]() ;
;
所以圆![]() 的方程为
的方程为![]() ,整理得:
,整理得: ![]() ;
;
因为![]() 为两圆的公共弦,两圆方程相减得:
为两圆的公共弦,两圆方程相减得: ![]() ;
;
所以![]() 为直线
为直线![]() 的方程;又因为
的方程;又因为![]() ;所以
;所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
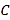 :
:  (
( )的两个焦点为
)的两个焦点为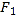 ,
, 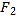 ,离心率为
,离心率为 ,点
,点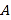 ,
, 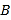 在椭圆上,
在椭圆上, 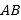 在线段
在线段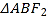 上,且
上,且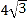 的周长等于
的周长等于 .
.(Ⅰ)求椭圆
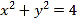 的标准方程;
的标准方程;(Ⅱ)过圆
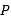 :
:  上任意一点
上任意一点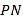 作椭圆
作椭圆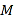 的两条切线
的两条切线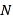 和
和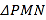 与圆
与圆 交于点
交于点 ,
, 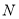 ,求
,求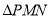 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
: 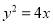 的焦点为
的焦点为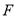 ,过点
,过点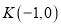 的直线
的直线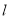 与
与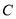 相交于
相交于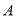 、
、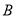 两点,点
两点,点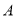 关于
关于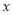 轴的对称点为
轴的对称点为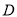 .
.(Ⅰ)判断点
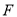 是否在直线
是否在直线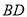 上,并给出证明;
上,并给出证明;(Ⅱ)设
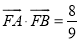 ,求
,求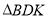 的内切圆
的内切圆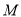 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入
 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )8
3
4
1
5
9
6
7
2
A. 9 B. 8 C. 6 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,其中
,其中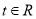 .
.(1)若
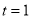 ,求函数
,求函数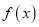 在区间
在区间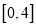 上的取值范围;
上的取值范围;(2)若
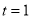 ,且对任意的
,且对任意的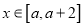 ,都有
,都有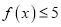 ,求实数
,求实数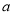 的取值范围;
的取值范围;(3)若对任意的
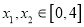 ,都有
,都有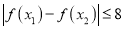 ,求实数
,求实数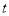 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
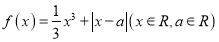 .
.(1)若函数
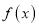 在
在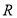 上为增函数,求
上为增函数,求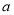 的取值范围;
的取值范围;(2)若函数
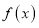 在
在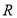 上不单调时;
上不单调时;①记
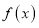 在
在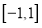 上的最大值、最小值分别为
上的最大值、最小值分别为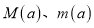 ,求
,求 ;
;②设
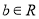 ,若
,若 ,对
,对 恒成立,求
恒成立,求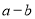 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设点
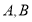 的坐标分别为
的坐标分别为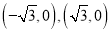 ,直线
,直线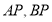 相交于点
相交于点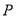 ,且它们的斜率之积为
,且它们的斜率之积为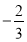 .
.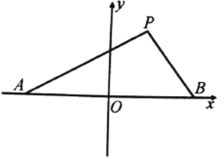
(1)求点
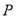 的轨迹方程;
的轨迹方程;(2)设点
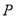 的轨迹为
的轨迹为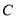 ,点
,点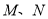 是轨迹为
是轨迹为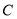 上不同于
上不同于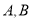 的两点,且满足
的两点,且满足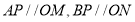 ,求证:
,求证: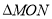 的面积为定值.
的面积为定值.
相关试题

