

【题目】已知集合![]() ,若对于任意
,若对于任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称集合
成立,则称集合![]() 是“
是“![]() 集合”.给出下列5个集合:
集合”.给出下列5个集合:
①![]() ;②
;②![]() ;③
;③![]() ;
;
④![]() ;⑤
;⑤![]() .
.
其中是“![]() 集合”的所有序号是( )
集合”的所有序号是( )
A.②③B.①④⑤C.②③⑤D.①②④
【答案】C
【解析】
根据集合![]() 是“
是“![]() 集合”,即满足曲线
集合”,即满足曲线![]() 上过任意一点与原点的直线,都存在过另一点与原点的直线垂直,逐项判定,即可求解.
上过任意一点与原点的直线,都存在过另一点与原点的直线垂直,逐项判定,即可求解.
由题意,集合![]() 是“
是“![]() 集合”,即满足曲线
集合”,即满足曲线![]() 上过任意一点与原点的直线,都存在过另一点与原点的直线垂直,
上过任意一点与原点的直线,都存在过另一点与原点的直线垂直,
对于①中,![]() ,假设集合
,假设集合![]() 是“
是“![]() 集合”,则存在两点
集合”,则存在两点![]() ,满足
,满足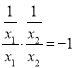 ,即
,即![]() ,方程无解,所以假设不成立,所以集合
,方程无解,所以假设不成立,所以集合![]() 不是“
不是“![]() 集合”;
集合”;
对于②中,函数![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,函数单调递增,当
,函数单调递增,当![]() 时,
时,![]() ,函数单调递减,且当
,函数单调递减,且当![]() 时,
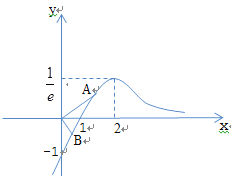
时,![]() ,图象如图所示,
,图象如图所示,
结合图象,可得对任意一点![]() ,总是存在一点
,总是存在一点![]() ,使得
,使得![]() 成立,
成立,
所以集合![]() 是“
是“![]() 集合”;
集合”;
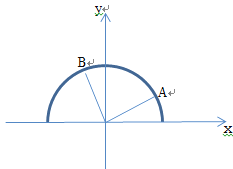
对于③中,集合![]() 的图象表示一个在
的图象表示一个在![]() 轴上方的半圆,
轴上方的半圆,
如图所示,根据圆的性质,可得对任意一点![]() ,总是存在一点
,总是存在一点![]() ,使得
,使得![]() 成立,
成立,
所以集合![]() 是“
是“![]() 集合”;
集合”;
对于④中,函数![]() ,当点
,当点![]() 时,
时,
若![]() ,则
,则![]() 不成立,
不成立,
所以集合![]() 不是“
不是“![]() 集合”;
集合”;
对于⑤中,函数![]() ,
,
设![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
则过原点且与![]() 垂直的直线
垂直的直线![]() 方程为
方程为![]() ,
,
直线![]() 与函数
与函数![]() 的图象必有交点,
的图象必有交点,
所以集合![]() 是“
是“![]() 集合”.
集合”.
故选:C.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: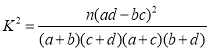 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),并以
为参数),并以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)写出![]() 的极坐标方程,并将
的极坐标方程,并将![]() 化为普通方程;
化为普通方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() 与
与![]() 相交于
相交于![]() 两点,
两点,
求![]() 的面积(
的面积(![]() 为圆
为圆![]() 的圆心).
的圆心).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,若椭圆上一点
,若椭圆上一点![]() 满足
满足![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]()
![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 轴的垂线,交椭圆
轴的垂线,交椭圆![]() 于
于![]() ,求证:
,求证: ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以椭圆长、短轴四个端点为顶点为四边形的面积为
,以椭圆长、短轴四个端点为顶点为四边形的面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
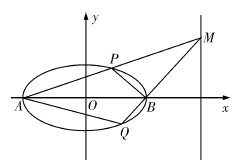
(Ⅱ)如图所示,记椭圆的左、右顶点分别为![]() 、
、![]() ,当动点
,当动点![]() 在定直线
在定直线![]() 上运动时,直线
上运动时,直线![]() 分别交椭圆于两点
分别交椭圆于两点![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥于2018年10月2刻日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55千米.桥面为双向六车道高速公路,大桥通行限速100km/h,现对大桥某路段上1000辆汽车的行驶速度进行抽样调查.画出频率分布直方图(如图),根据直方图估计在此路段上汽车行驶速度在区间[85,90)的车辆数和行驶速度超过90km/h的频率分别为( )
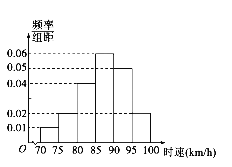
A. 300,![]() B. 300,
B. 300,![]() C. 60,
C. 60,![]() D. 60,
D. 60,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,…,
,…,![]() 为取自某总体的样本,其算术平均值称为样本均值,一般用
为取自某总体的样本,其算术平均值称为样本均值,一般用![]() 表示,即
表示,即![]() ,在分组样本场合,样本均值的近似公式为
,在分组样本场合,样本均值的近似公式为![]() ,其中k为组数,
,其中k为组数,![]() 为第i组的组中值,
为第i组的组中值,![]() 为第i组的频数.某单位收集到20名青年的某天娱乐支出费用数据:
为第i组的频数.某单位收集到20名青年的某天娱乐支出费用数据:
79 84 84 88 92 93 94 97 98 99
100 101 101 102 102 108 110 113 118 125
若将分为五组,第一组为![]() ,根据分组样本计算样本均值为( )
,根据分组样本计算样本均值为( )
A.99.4B.143.16C.100D.11.96
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com