【题目】如图,直四棱柱![]() 底面
底面![]() 直角梯形,
直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(2)求证:![]() 平面
平面![]() .
.
参考答案:
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)本题中由于有![]() 两两垂直,因此在求异面直线所成角时,可以通过建立空间直角坐标系,利用向量的夹角求出所求角;(2)同(1)我们可以用向量法证明线线垂直,以证明线面垂直,
两两垂直,因此在求异面直线所成角时,可以通过建立空间直角坐标系,利用向量的夹角求出所求角;(2)同(1)我们可以用向量法证明线线垂直,以证明线面垂直,![]() ,
,![]() ,
,![]() ,易得
,易得![]() 当然我们也可直线用几何法证明线面垂直,首先
当然我们也可直线用几何法证明线面垂直,首先![]() ,这由已知可直接得到,而证明
,这由已知可直接得到,而证明![]() 可在直角梯形
可在直角梯形![]() 通过计算利用勾股定理证明,
通过计算利用勾股定理证明,![]() ,
,![]() ,因此
,因此![]() ,得证.
,得证.
(1)以![]() 原点,
原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则![]() ,
,![]() ,
,![]() ,
,![]() . 3分
. 3分
于是![]() ,
,![]() ,
,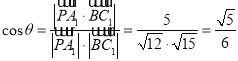 ,
,
![]() 异面直线
异面直线![]() 与
与![]() 所成的角的大小等于
所成的角的大小等于![]() . 6分
. 6分

(2)过![]() 作
作![]() 交
交![]() 于
于![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]() 10分
10分
![]() ,
,![]() .又
.又![]() ,
,![]()
![]() 平面
平面![]() . 12分
. 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 .
.(1)求f(2)与f
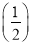 , f(3)与f
, f(3)与f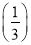 ;
;(2)由(1)中求得结果,你能发现f(x)与f
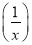 有什么关系?并证明你的发现;
有什么关系?并证明你的发现;(3)求f(1)+f(2)+f(3)+…+f(2013)+f
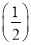 +f
+f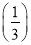 +…+f
+…+f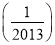 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,知识告知大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”.

(1)求乙班总分超过甲班的概率;
(2)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分,
①请你从平均分和方差的角度来分析两个班的选手的情况;
②主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为
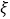 ,求
,求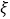 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应市政府“绿色出行”的号召,王老师每个工作日上下班由自驾车改为选择乘坐地铁或骑共享单车这两种方式中的一种出行.根据王老师从2017年3月到2017年5月的出行情况统计可知,王老师每次出行乘坐地铁的概率是0.4,骑共享单车的概率是0.6.乘坐地铁单程所需的费用是3元,骑共享单车单程所需的费用是1元.记王老师在一个工作日内上下班所花费的总交通费用为X元,假设王老师上下班选择出行方式是相互独立的.
(I)求X的分布列和数学期望
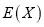 ;
;(II)已知王老师在2017年6月的所有工作日(按22个工作日计)中共花费交通费用110元,请判断王老师6月份的出行规律是否发生明显变化,并依据以下原则说明理由.
原则:设
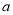 表示王老师某月每个工作日出行的平均费用,若
表示王老师某月每个工作日出行的平均费用,若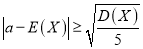 ,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注:
,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注: 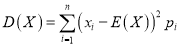 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
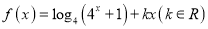 是偶函数.
是偶函数.(1)求
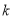 的值;
的值;(2)设
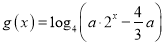 ,若函数
,若函数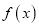 与
与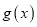 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数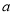 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.
指数
级别
类别
户外活动建议
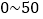
Ⅰ
优
可正常活动
Ⅱ
良
Ⅲ
轻微污染
易感人群症状有轻度加剧,健康人群出现刺激症状,心脏病和呼吸系统疾病患者应减少体积消耗和户外活动.
轻度污染
Ⅳ
中度污染
心脏病和肺病患者症状显著加剧,运动耐受力降低,健康人群中普遍出现症状,老年人和心脏病、肺病患者应减少体力活动.
中度重污染
Ⅴ
重污染
健康人运动耐受力降低,由明显强烈症状,提前出现某些疾病,老年人和病人应当留在室内,避免体力消耗,一般人群应尽量减少户外活动.
现统计邵阳市市区2016年1月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图.
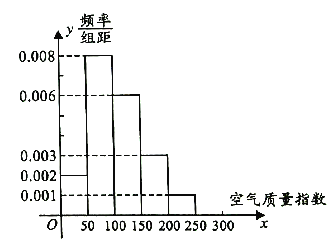
(1)求这60天中属轻度污染的天数;
(2)求这60天空气质量指数的平均值;
(3)一般地,当空气质量为轻度污染或轻度污染以上时才会出现雾霾天气,且此时出现雾霾天气的概率为
 ,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B.
(Ⅰ)若∠APB=60°,试求点P的坐标;
(Ⅱ)若P点的坐标为(2,1),过P作直线与圆M交于C,D两点,当CD=
 时,求直线CD的方程.
时,求直线CD的方程.
相关试题

