【题目】若x=2是函数f(x)=x(x﹣m)2的极大值点,则m的值为( )
A.3
B.6
C.2或6
D.2
参考答案:
【答案】B
【解析】解:f(x)=x(x﹣m)2=x3﹣2mx2+m2x,则f′(x)=3x2﹣4mx+m2 ,
x=2是函数f(x)的极大值点,
f′(2)=0,12﹣8m+m2=0,解得m=2或6,
当m=2时,f(x)=x(x﹣2)2 , f′(x)=3x2﹣8x+4,
f′(x)>0,解得:x>2或x< ![]() ,
,
f′(x)<0,解得: ![]() <x<2,
<x<2,
∴f(x)的单调递增区间为:(﹣∞, ![]() ),(2,+∞),单调递减区间为:(
),(2,+∞),单调递减区间为:( ![]() ,2),
,2),
∴x= ![]() 是f(x)的极大值,x=2是f(x)的极小值;
是f(x)的极大值,x=2是f(x)的极小值;
当m=6时,f(x)=x(x﹣6)2 , f′(x)=3x2﹣24x+36,
f′(x)>0,解得:x>6或x<2,
f′(x)<0,解得:2<x<6,
∴f(x)的单调递增区间为:(﹣∞,2),(6,+∞),单调递减区间为:(2,6),
∴x=2是f(x)的极大值,x=6是f(x)的极小值;
所以m=6,
故答案选:B.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A,B为曲线C:y=
 上两点,A与B的横坐标之和为4.
上两点,A与B的横坐标之和为4.(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM
 BM,求直线AB的方程.
BM,求直线AB的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:
 ,并绘制成如图所示的频率分布直方图.
,并绘制成如图所示的频率分布直方图.(1)求该社区参加健美操运动人员的平均年龄;
(2)如果研究小组从该样本中年龄在
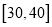 和
和 的6人中随机地抽取出2人进行深入采访,求被采访的2人,年龄恰好都在
的6人中随机地抽取出2人进行深入采访,求被采访的2人,年龄恰好都在 内的概率.
内的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C的参数方程是
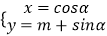 (α为参数),直线l的参数方程为
(α为参数),直线l的参数方程为  (t为参数),
(t为参数),
(1)求曲线C与直线l的普通方程;
(2)若直线l与曲线C相交于P,Q两点,且|PQ|=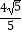 ,求实数m的值.
,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a为实常数,y=f(x)是定义在R上的奇函数,当x<0时
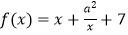 ,若f(x)≥a+1对一切 x≥0成立,则a的取值范围为 .
,若f(x)≥a+1对一切 x≥0成立,则a的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】对于R上的可导函数f(x),若a>b>1且有(x﹣1)f′(x)≥0,则必有( )
A.f(a)+f(b)<2f(1)
B.f(a)+f(b)≤2f(1)
C.f(a)+f(b)≥2f(1)
D.f(a)+f(b)>2f(1) -
科目: 来源: 题型:
查看答案和解析>>【题目】以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角性”.

该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
A.2017×22015
B.2017×22014
C.2016×22015
D.2016×22014
相关试题

